データサイエンティスト(仮)

元素粒子論博士。今はデータサイエンティスト（仮）。

Pythonでデータ分析：Auto-sklearnについてのメモ

auto-sklearn Python

導入

最近、Meta Learningという考えに少し興味を持ちました。もともとは認知科学発祥の考えですが、機械学習の文脈だと

ある決まったバイアス，すなわち仮説空間の中から，事例に応じて，適切な仮説を獲得する普通の学習器をベース学習器という．その上位で，学習対象のタスクやドメインに応じて，学習器のバイアスを決定するためのメタ知識を獲得するのがメタ学習 (meta learning)．

メタ学習 - 機械学習の「朱鷺の杜Wiki」
という概念のようです。ざっくりいうと、学習のためのメタな学習規則を学習する（Learning to learn）という感じなのかなと思います。

このMeta Learningですが、機械学習の自動化、つまりあるデータセットを投入すると「良い」機械学習モデルを自動で作成すること、とも関係しているようです。こういった背景のもと、そういえばAuto-sklearnってMeta Learningが取り入れられていなかったっけ、とふと思い出し、中の仕組みって大まかにどうなっているんだろうというのが気になりました。そういった経緯で、Auto-sklearnのベースになった論文を調べてみたメモを、備忘録として記事に残しておくことにしました。

Auto-sklearn

Auto-sklearnは自動で機械学習のモデルを構築してくれるPythonのライブラリです。
github.com

ざっくりした概要やインストール方法は、過去に自分が紹介していたようです。
tekenuko.hatenablog.com
この記事を見ると、詳しくは以下のページといって実質元論文に投げてしまってます。過去の自分はしょうもないことやってるな。

Auto-sklearnのベース論文

Auto-sklearnの仕様やパフォーマンスが紹介されている論文は、以下のNIPS 2015での論文です。
papers.nips.cc
概要はこれを見ると載っているのですが、細かい話は「Supplementary MaterialのTableやFigにある」という記載が度々見られます。Supplement Materialってなんだろうと思ってネット検索をしてみると、以下の文献がヒットします。どうやらこれがSupplementary Materialのようです。
https://pdfs.semanticscholar.org/699c/12c4b47b7dff4c9ae9b22b9326ae9a1dacca.pdf

Auto-sklearnの概観

Auto-sklearnの全体感は以下になります。
f:id:tekenuko:20171212230243p:plain
Auto-sklearnの自動化部分は図の「AutoML system」になります。大まかな構造は以下のようになっています。

  • Meta Learning部分
  • ML framework部分
  • Build ensenble部分

ML framework部分でベイズ的最適化を用いて良いモデルを選択する、という方法は、Auto-WEKAですでに取り入れられているようです。
Auto-WEKA
ただ、Auto-WEKAだと探索するパラメータが多すぎる、アンサンブルを取ったモデルも含めて探索する、といった非効率性が欠点としてあったため、Auto-sklearnではMeta Learning部分とBuild ensanble部分を加えた3部構成にしているようです。

Meta Learning

この部分は、「効率性」に着目した部位です。高精度の機械学習モデルを自動的に構築する場合、前処理、特徴量エンジニアリングの方法、機械学習アルゴリズム、ハイパーパラメータといった膨大な選択肢をしらみつぶしに探していかなければなりません。コンピュータのリソースや時間が潤沢にあればこういった探索を行ってもよいですが、実際にはリソースに限りがあることが多く、制約がある中で効率的に良いもの探していく必要があります。その際に効率的に探す指針を与えてくれるのが、このMeta Learning部分です。

大まかには、この部分では以下のような操作が行われています。

  • あらかじめ、OpenMLの140のデータセット（https://www.openml.org/search?type=data）から、後述のMeta Feature、およびベイズ的最適化による「ML framework」（前処理、特徴量エンジニアリング、分類器選択のセット）を抽出
  • 新しいデータセット：今回モデル構築したいデータを投入した際は、データからMeta Featureを算出、Meta Featureの空間でOpenMLのデータセットとのL_1距離を計算
  • 距離が近いものから25種類のML frameworkを選択し、それらをベースに次段のベイズ的最適化へ移行

データセットから計算するMeta Featureは以下のようです。基本的には、要約統計量や次元圧縮に関連する量、エントロピーなどがMeta Featureとなっているようです。
f:id:tekenuko:20171212222410p:plain

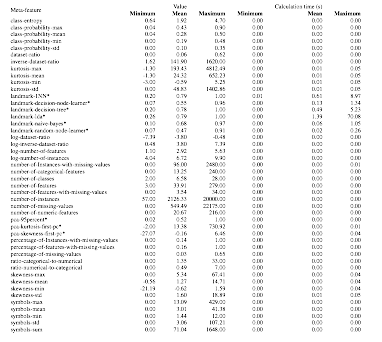
ML framework

ここでは、前段で選択された候補に関して処理を行います。論文の図をべた張りですが、前処理や分類器の候補は以下になります。
f:id:tekenuko:20171212222927p:plain
これらと、前段で絞りこんだ情報をもとに、ベイズ的最適化によりよいものを選択します。評価に関しては、あらかじめ評価指標を設定しておきます。
f:id:tekenuko:20171212223245p:plain

Build ensenble

Auto-sklearnでは、結果をロバストにするために、ML framework部分で算出した結果のアンサンブル平均をとっています。単に足し合わせるのではなく、精度向上に効果があるものを貪欲に入れ込んでいく、としているようです。
f:id:tekenuko:20171212223424p:plain

Auto-sklearnの性能

（ここの解釈は、若干誤解しているかもしれませんので、修正が入るかもしれません。）
論文での性能比較の表は以下です。
f:id:tekenuko:20171212224314p:plain
f:id:tekenuko:20171212224345p:plain
上の表がアルゴリズム間での比較、下の表が前処理方法間での比較です。数字が低いほど良いという見方です。結果を見ると、最も良いパフォーマンスではないが、安定して良い結果になっているという印象です。なので思考停止的にデータを投入してもそこそこの結果が出て来るというものになっているようです。とっても個人的なバイアスがかかっている意見だと思いますが、DataRobotみたいだな、と思いました。
www.datarobot.com
（といいつつDataRobotは黒魔術モデルまで込みで一番いいのを頼む、という感じなので、Auto-WEKAに近しいのかな）

まとめ

今回は、Auto-sklearnについて大まかな処理内容を紹介しました。機械学習のモデルに関して詳細を知らなくてもそこそこ良い結果が出る仕組みを作ったのは素晴らしいことだと思います。さらに、論文が出た時点では分類問題のみが対象でしたが、現在は回帰についても取り扱えるようです。こういった簡単に機械学習ができる仕組みが発達していき、活用のハードルが下がった結果、機械学習の活用シーンが広がって行くことを期待します。

Pythonでデータ分析：imbalanced-learnで不均衡データのサンプリングを行う

Python

導入

クラス分類、例えば0：負例と1：正例の二値分類を行う際に、データが不均衡である場合がたびたびあります。例えば、クレジットカードの取引データで、一つの取引に対して不正利用かどうか（不正利用なら1、それ以外は0）といった値が付与されているカラムがあるとします。通常、不正利用というのは稀に起こる事象なので、不正利用かどうかが格納されているカラムに関してはほとんどが0で、1がほとんどない、という状況になりがちです。

上記の状況で不正利用を予測するようなモデル構築をする場合、目的変数として不正利用かどうかを用いることになりますが、0と1の比率が50%から極度に乖離します（1の比率が0.X%とかになる）。こういったデータで予測モデルを構築すると、往々にして負例だけを予測する（予測値がすべて0になる）モデルになりがちです。というのは、不均衡なデータの場合はそれでも「正解率（Accuracy）」が高くなってしまうからです。例えば、目的変数の内訳が、0が99990件、1が10件の場合に、すべて0と出力するモデルができたとすると、正解率は99990 / (99990 + 10) = 99.99%となります。このモデルは正解率は高いのですが、すべての不正利用を見逃す（偽陰性：本当は不正利用（=1）だけれども不正利用でない（=0）と誤って予測する）ことになり、不正利用を検知したいという目的には全くそぐわないモデルになっています。

不正利用を予測したい、つまり誤検出が多少増えてもから不正利用を検出したいという状況では、サンプリングによって正例と負例の割合を変える、といった方法が採られます。つまり、学習に使われる正例の割合を増やすことで偽陰性を減らし、多少の偽陽性（本当は不正利用していない（=0）けれども不正利用（=1）と誤って予測する）は出しつつも不正利用も検出できるようにします。割合を変化させるにあたって、大きく以下の3パターンがあります。

  • Under Sampling：負例を減らす
  • Over Sampling：正例を増やす
  • 上記の両方を行う

これら割合の変化は、Pythonではimbalanced-learnというライブラリを用いると簡単に行えます。今回は、このimbalanced-learnを用いてUnder/Over Samplingをどう行うかを簡単に紹介します。

ライブラリのインストール

pipが利用できるなら、以下のように簡単にインストールできます。

$ pip install -U imbalanced-learn

開発版を使用したい場合は、githubからインストールします。

$ git clone https://github.com/scikit-learn-contrib/imbalanced-learn.git
$ cd imbalanced-learn
$ python setup.py install

サンプルデータ

不均衡データを人工的に生成します。こういった人工データは、sklearn.datasets.make_classificationを用いると簡単に作成できます。今回、10万件のデータで、正例が10件のデータを以下のようにして作成しました。

from sklearn.datasets import make_classification
df = make_classification(
    n_samples = 100000, n_features = 10, n_informative = 2, n_redundant = 0, 
    n_repeated = 0, n_classes = 2, n_clusters_per_class = 2, weights = [0.9999, 0.0001], 
    flip_y = 0, class_sep = 1.0, hypercube = True, shift = 0.0, 
    scale = 1.0, shuffle = True, random_state = 71)

パラメータの意味は以下です。今回大事なのは、n_sample, n_classes, weightsの3つで、あとはえいやっと決めています。

パラメータ名 説明
n_samples 生成するサンプルの数
n_features 生成する特徴量の数
n_informative 目的変数のラベルと相関が強い特徴量(Informative fearture）の数
n_redundant Informative featureの線形結合から作られる特徴量(Redundant fearture）の数
n_repeated Infomative、Redundant featureのコピーからなる特徴量の数(Repeated feature)
n_classes 分類するクラス数
n_clusters_per_class 1クラスあたりのクラスタ数
weights クラスの比率で、例えば、2値分類問題の場合、Noneとすると0と1が50%ずつだが、[0.9, 0.1] と与えると0が90%、1が10%になる
flip_y クラスのフリップ率で、例えば0.01とすると各クラスの1%の符号がランダムに変更される
class_sep 生成アルゴリズムに関係するパラメータ（細かい話はドキュメント参照）
hypercube 生成アルゴリズムに関係するパラメータ（細かい話はドキュメント参照）
shift 全ての特徴量にshiftを加算する。Noneが指定された場合、[-class_sep, class_sep]の一様乱数を加算する
scale 全ての特徴量にscaleを乗算、Noneが指定された場合、 [1, 100]の一様乱数を乗算する
shuffle Trueにすると行と列をシャッフルする
random_state 乱数を制御するパラメータで、Noneにすると毎回違うデータが生成されが、整数をシードとして渡すと毎回同じデータが生成される

sklearn.datasets.make_classification — scikit-learn 0.19.1 documentation

あとは申し訳程度にDataFrameに変換してカラム名などをつけておきます。ここは、私がcsvにいったん保存したりする関係で行った操作なので、必須ではないです。

import numpy as np
import pandas as pd
from pandas import DataFrame, Series
df_raw = DataFrame(df[0], columns = ['var1', 'var2', 'var3', 'var4', 'var5', 'var6', 'var7', 'var8', 'var9', 'var10'])
df_raw['Class'] = df[1]

クラスの割合は、以下のようになっています。

df_raw['Class'].value_counts()

# 出力
0    99990
1       10
Name: Class, dtype: int64

圧倒的に0が多くなっています。

プロトタイプモデル作成

不均衡データをサンプリングしないまま、分類のためのロジスティック回帰モデルを作成してみます。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix

# 学習用と検証用に分割
X = df_raw.iloc[:, 0:10]
y = df_raw['Class']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 71)

# モデル構築
mod = LogisticRegression()
mod.fit(X_train, y_train)

# 予測値算出
y_pred = mod.predict(X_test)

正解率（Accuracy）は、以下になります。

print('Accuracy(test) : %.5f' %accuracy_score(y_test, y_pred))

# 出力
Accuracy(test) : 0.99990

このように、正解率99.99%という、一見精度が良さそうなモデルができています。

しかし、混同行列を出力してみると

tn, fp, fn, tp = confusion_matrix(y_test, y_pred).ravel()
(tn, fp, fn, tp)

# 出力
(29997, 0, 3, 0)

のように、TN（正でない（=0）ものを正でない（=0）と予測する）とFN（本当は正（=1）だが正でない（=0）と誤って予測する）のみに値があり、FP（本当は正でない（=0）ものを正である（=1）と誤って予測する）とTP（正である（=1）ものを正である（=1）と予測する）が0となっています。つまり、単にすべて0と予測するモデルになっています*1。

Precision（正と予測したデータのうち，実際に正であるものの割合：TP / （TP + FP））とRecall（実際に正であるもののうち，正であると予測されたものの割合：TP / （TP + FN））を評価してみます。

print('precision : %.4f'%(tp / (tp + fp)))
print('recall : %.4f'%(tp / (tp + fn)))

# 出力
precision : nan
recall : 0.0000

計算が不能になっているか、0になっているという、ひどい結果です。まあ実質意味のある予測ができるモデルではありませんからね…。

Under Sampling

ここでは、負例を減らして結果がどう変わるかを見てみます。imbalanced-learnで提供されているRandomUnderSamplerで、負例サンプルをランダムに減らし、正例サンプルの割合を10%まで上げます。

# ライブラリ
from imblearn.under_sampling import RandomUnderSampler

# 正例の数を保存
positive_count_train = y_train.sum()
# print('positive count:{}'.format(positive_count_train))とすると7件

# 正例が10％になるまで負例をダウンサンプリング
rus = RandomUnderSampler(ratio={0:positive_count_train*9, 1:positive_count_train}, random_state=71)

# 学習用データに反映
X_train_resampled, y_train_resampled = rus.fit_sample(X_train, y_train)

あとはプロトタイプモデル作成の際と同様、ロジスティック回帰モデルを構築し、性能を見てみます。

# モデル作成
mod = LogisticRegression()
mod.fit(X_train_resampled, y_train_resampled)

# 予測値算出
y_pred = mod.predict(X_test)

# Accuracyと混同行列
print('Confusion matrix(test):\n{}'.format(confusion_matrix(y_test, y_pred)))
print('Accuracy(test) : %.5f' %accuracy_score(y_test, y_pred))

# 出力
Accuracy(test) : 0.96907
Confusion matrix(test):
[[29070   927]
 [    1     2]]

# PrecisionとRecall
tn, fp, fn, tp = confusion_matrix(y_test, y_pred).ravel()
print('precision : %.4f'%(tp / (tp + fp)))
print('recall : %.4f'%(tp / (tp + fn)))

# 出力
precision : 0.0022
recall : 0.6667

正解率は落ちたものの、PrecisionとRecallが0でない値になりました。混同行列を見ても、TPが0でなくなっており、FNが小さくなっていることがわかります。しかし、その代償としてFPが927件と大きくなってしまい、それが小さいPrecisionとして跳ね返っています。

Over Sampling

今度は逆に正例を水増しして正例サンプルの割合を10%まで上げます。imbalanced-learnで提供されているRandomOverSamplerで行います。

# ライブラリ
from imblearn.under_sampling import RandomOverSampler

# 正例を10％まであげる
ros = RandomOverSampler(ratio = {0:X_train.shape[0], 1:X_train.shape[0]//9}, random_state = 71)

# 学習用データに反映
X_train_resampled, y_train_resampled = ros.fit_sample(X_train, y_train)

Under Samplingの場合と同様、モデルを作成して性能を見てみます。

# モデル作成
mod = LogisticRegression()
mod.fit(X_train_resampled, y_train_resampled)

# 予測値算出
y_pred = mod.predict(X_test)

# Accuracyと混同行列
print('Confusion matrix(test):\n{}'.format(confusion_matrix(y_test, y_pred)))
print('Accuracy(test) : %.5f' %accuracy_score(y_test, y_pred))

# 出力
Accuracy(test) : 0.98983
Confusion matrix(test):
[[29693   304]
 [    1     2]]

# PrecisionとRecall
tn, fp, fn, tp = confusion_matrix(y_test, y_pred).ravel()
print('precision : %.4f'%(tp / (tp + fp)))
print('recall : %.4f'%(tp / (tp + fn)))

# 出力
precision : 0.0065
recall : 0.6667

Under Samplingの場合と比較して、FPの数が若干抑えられており（304件）、Precisionが若干良くなっています。

SMOTE

上記のOver Samplingでは、正例を単に水増ししていたのですが、負例を減らし、正例を増やす、といった考えもあります。こういった方法の一つに、SMOTE（Synthetic Minority Over-sampling Technique）というアルゴリズムがあります。imbalanced-learnでは、このSMOTEも提供されているので、ここでも試してみます。

# ライブラリ
from imblearn.over_sampling import SMOTE

# SMOTE
smote = SMOTE(ratio={0:X_train.shape[0], 1:X_train.shape[0]//9}, random_state=71)
X_train_resampled, y_train_resampled = smote.fit_sample(X_train, y_train)

# モデル作成
mod = LogisticRegression()
mod.fit(X_train_resampled, y_train_resampled)

# 予測値算出
y_pred = mod.predict(X_test)

# Accuracyと混同行列
print('Confusion matrix(test):\n{}'.format(confusion_matrix(y_test, y_pred)))
print('Accuracy(test) : %.5f' %accuracy_score(y_test, y_pred))

# 出力
Accuracy(test) : 0.98923
Confusion matrix(test):
[[29675   322]
 [    1     2]]

# PrecisionとRecall
tn, fp, fn, tp = confusion_matrix(y_test, y_pred).ravel()
print('precision : %.4f'%(tp / (tp + fp)))
print('recall : %.4f'%(tp / (tp + fn)))

# 出力
precision : 0.0062
recall : 0.6667

Under SamplingとOver Samplingの間くらいの性能になりました。Under/Over Samplingを両方合わせ技でやっているので、直感的にはそうなるんですかね。

まとめ

今回は、Pythonのライブラリで不均衡データの取扱いについて紹介しました。今回はOver Samplingが一番有効でありましたが、データが与えられたときに有力な手法はそのデータの性質に依存する部分も大きいです。なのでどういったサンプリングがよいかは、都度色々試してみて決める必要があります。

また、今回紹介したimbalanced-learnには、上記の3つ以外にもサンプリングの方法が実装されています。今回はそのすべてを紹介できませんでしたが、どういったものがあるかは、以下のページを参照していただければと思います。
imbalanced-learn API — imbalanced-learn 0.3.0 documentation

*1:この結果を出すためにseedを調整していたり…。

Dynamic Routing Between Capsulesを読む

Deep Learning

前提

この記事はDeepLearning論文紹介 Advent Calendar 2017 - Adventarの12月10日の記事です。Advent Calendarで記事を書くのは初めてですが、頑張ります。理解が足りなくて非常にわかりづらい記事になっていると思いますので、今後もちょくちょく修正が入ると思います。

読んだ論文

Hintonさんが著者に入っている、以下の論文です。
[1710.09829] Dynamic Routing Between Capsules
Deep Learning界の重鎮のアイデアということもあり、興味を持ったため、こちらの論文を読むことにしました。

概要

正直、Introductionは門外漢すぎてあまり腹落ちしていないのですが、より人間の脳に近しいと思われるネットワーク構造を考え、CNNよりも人間の認知に近いような分類器を作ろうという試みのようです。そのための一歩として、内積やスカラー値の塊であった層をベクトルの塊であるcapsuleというものに置き換え、capsuleを用いたネットワークであるCapsNetを提唱している論文になります。

現在、物体認識ではCNNを用いることがスタンダードに見えますが、以下の記事のHintonの講義にあるように、欠点もあるようです。
Dynamic Routing Between Capsules | moskomule log
大きくは

  • poolingで微小変換に対する不変性を獲得する代わりに、顔→目, 鼻といった位置情報、階層構造が失われる
  • 回転などの差異を識別するために別途学習データが必要

といったものです。本論文で提唱している、capsuleを組み込んだCapsNetでは、位置や姿勢などの情報をcapsuleというベクトルの形で保持し，capsule同士が階層的な「構文木」をなすように結合の仕方（routing）を学習することで、CNNの欠点を解消できる可能性があります。

以下、CapsNetの構造、および検証結果について紹介していきます。

Capsuleの計算の入出力

capsuleのimplementationの方法にはいくつか方法があるようですが、論文ではCapsNetのアイデアのキモになる部分、capsuleの入出力とcapsule間の関係を決める方法にフォーカスして紹介しています。

squashing：capsuleの入出力

capsuleでは、capsuleの出力ベクトルの長さが対応するものの存在確率を表現するようにしています。通常のニューラルネットワークでは、活性化関数でそういった効果を表現しますが、capsuleでは以下のような「squashing」という変換でベクトルの長さを|0, 1)にして表現しているようです。
$$
\vec{v}_l = \frac{ \| \vec{s}_j \|^2}{1 + \| \vec{s}_j \|^2} \frac{\vec{s}_j}{\| \vec{s}_j \|}
$$
ここで、\vec{v}_j はcapsule jの出力ベクトルで、\vec{s}_j はそのcapsuleに対する入力です。

Routing：capsule間の関係性

\vec{s}_j は、前層のcapsuleとの結びつきによって決まります。前層のi番目*1capsuleの出力を\vec{u}_i, 次の層のj番目のcapsuleとの「重み行列」をW_{ij}とします*2。これらを掛け合わせたものを「prediction vector」\hat{\vec{u}}_{j|i}とし、各iに対して重みつけ和をとったものが\vec{s}_j となります。
$$
\vec{s}_j = \sum _i c_{ij} \hat{\vec{u}}_{j|i}
$$
係数c_{ij}は、c_{ij}は、以下のようなsoftmaxの形をしています。
$$
c_{ij} = \frac{\text{exp}(b_{ij})}{\sum_k \text{exp}(b_{ik})}
$$
ロジットb_{ik}は以下のroutingアルゴリズムによって動的に更新されます。

f:id:tekenuko:20171210152049p:plain

「Agreement」\hat{\vec{u}}_{j|i} \cdot \vec{s}_j はcapsule間の類似度的な量になっていると考えられます。この量を用いてロジットを更新していくため、結びつきが強そうなcapsule間の係数c_{ij}がどんどん1に、そうでない係数は0に近づいていくような動きをするのでしょう。

ここの解釈に関して、以下のブログでこのような例えがありました。
f:id:tekenuko:20171210160729p:plain
Dynamic Routing Between Capsules | moskomule log

CapsNetのアーキテクチャー

CapsNetのアーキテクチャーは以下になります。
f:id:tekenuko:20171208113058p:plain:w800
中間層は全3層で、2層が畳み込み層、1層が全結合層です。2層目と3層目がCapsuleになっています。

  • 1層目：畳み込み層
    • channel（フィルタの数）：256
    • kernel（フィルタのサイズ）：9×9
    • stride（畳み込みの際にスライドさせるピクセルの間隔）：1
    • 活性化関数：ReLU
    • 出力：20×20×256
  • 2層目：畳み込みCapsule（PrimaryCapsules）
    • Capsuleの数：32
    • channel（Capsuleのベクトルの成分数）：8
    • kernel：9×9
    • stride：2
    • squashing
  • 3層目：全結合Capsule（DigitCaps）
    • Capsuleの数：10（クラス数10に対応）
    • Capsuleのベクトルの成分数：16

Loss関数

Margin Lossを採用。各クラスに対応するcapsuleに対し
$$
L_k = T_k \ \text{max}\left( 0, m^+ \|\vec{v}_k \| \right)^2 + \lambda \left( 1 - T_k \right) \ \text{max}\left( 0, \|\vec{v}_k \| - m^- \right)^2
$$
としています。T_k はクラスkが存在する場合は1をとり、m^+ = 0.9, \ m^- = 0.1, \lambda = 0.5ととっています。全体のLossはすべてのcapsuleのLossの和をとったものを使用します。

routingの実装について

Tensorflowで実装し、OptimizerはAdamを使用しているとのことです。パラメータはTensorflowのデフォルトを使用、学習率は指数的に落ちていくようになっているようです。

正則化による再構成

本論文では、Margin Lossに加えて、以下の構造を使った入力画像と再構成した出力による二乗誤差を新たに追加しているようです。
f:id:tekenuko:20171210162726p:plain:w500
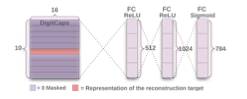
最終層の次元が784なのは、MNISTの入力の28×28 = 784に対応しています。加える際には、0.0005を掛けてから追加しているようです。再構成した画像が入力に近くない場合は、大きな二乗誤差が出ることになるため、ネットワークが入力画像に近い画像を出せるような重みになることを期待し、またそのような重みに学習が進むことをエンカレッジしているような考えなんだと思います。

再構成できているかの図が一つ紹介されていますが、5と3が間違えやすいということはあれど、概ねよく再現されているのでしょう。
f:id:tekenuko:20171210172856p:plain:w500

実験結果

CapsNetの性能に関しては、主にMNISTとMultiMNIST（MNISTの数字を重ねたもの）を用いて伝統的なCNNとの比較を行っています。

結果のまとめは以下となります。
f:id:tekenuko:20171210164000p:plain:w500

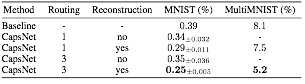
Baselineは、畳み込み層の数は3つで、channel数がそれぞれ256, 256, 128, kernelとstrideは5×5と1に統一しています。畳み込み層のあとは328次元、192次元の全結合層で、最後にdropoutを利用した出力層、という構造になっており、Loss関数はクロスエントロピーを使用しています。OptimizerはAdamを使用しているようですが、細かいパラメータの話は記載がありません。routingの実装の際と同様、デフォルトのパラメータを使用しているのだと思います。

MNIST

CapsNetはデータ拡張やデータの回転、スケーリング、アンサンブルを用いずにテストエラー0.25%を達成しています。先行研究（アンサンブルなどを使用）の0.21%と近しい精度となっており、routingが精度向上に寄与しているのではないかと考えられます。また、CapsNetは従来のCNNと比較してパラメータ数が少なく（Baselineは35.4M個、CapsNetは再構成を除くと6.8M、含めても8.2M）、効率的な学習ができていると見ることもできそうです。

また、学習で獲得したDigitCapに関して、16次元のベクトルの要素を少しずつ動かした結果が以下になります。
f:id:tekenuko:20171210173131p:plain:w500
太さやスケールの変換を性質として持つような成分が獲得されているような振る舞いになっています。これはとても面白い性質だと思います。

Affine変換に対するロバスト性

また、CapsNetが画像の変換に対してロバストかを検証するために、MNISTをアフィン変換（伸縮・回転・平行移動）をしたデータセット（affNIST）に関してテストを実施しています。以下は、affNISTの画像の例です。
f:id:tekenuko:20171210170936p:plain:w300
あらかじめCapsNetとCNN（畳み込み層＋プーリング層とDropout層）でMNISTによってそれぞれ訓練データの精度を99.2~3%となるまで学習します。これらをaffNISTでテストした結果、それぞれ精度が79%, 66%となっており、CapNetのほうがよい性能を出しています。よって、従来のCNNよりもCapsNetが変換に対してロバストであると期待されます。

MultiMNIST

本論文では、MNISTの画像を重ねたもの（MultiMNIST）に関しても検証を行っています。以下は重ねたものに関して分離できているかを表す図です。
f:id:tekenuko:20171210171923p:plain:w500
R(,) が再構築をする際に使ったラベル、L(,) が正解のラベルを表しています。 白黒の画像はMultiMNISTの画像で、数字が2つ重なっています、カラフルな画像は下は再構築した画像で、R(,) のラベルを1つずつ使って再構築した画像を色違いで重ねています。重なっている場合でも概ねうまくラベル付けできるようです。

他のデータセット

CIFAR 10やsmallNORB、SVHMといったデータセットでも検証を行っています。ただし、例えばCIFAR 10では7モデルのアンサンブルによってテストエラー10.6%を達成しているなど、アンサンブルを行っています。そういった操作を行わない場合の性能が気になります。

Discussionと所感

CapsNetは、2000年代はじめの音声認識によるRNNと似たような研究段階にあるとの主張をしています。結構アナロジーがあるようです。音声認識では隠れマルコフがかつては有用な方法だったが、スケールすると非効率な点があり、再帰型のネットワークの研究が登場し、とって変わられたという歴史があるようですが*3、物体認識に関するCNNとcapsuleの関係も似たものである可能性があります。CNNは回転や平行移動はデータを水増しして学習する必要があるので、リッチな認識性能を獲得するためにはどんどん学習データを増やさなくてはいけません。一方で、capsuleは変換や重なりといった構造を少ないコストで獲得することが期待されるもので、研究が進めば物体認識でCNNにとって変わる存在になるかもしれません。正直、capsuleそのものや論文に関してきちんと理解ができていない部分があったり疑問点もありますが、将来非常に有用なものになる可能性を感じました。今後の研究の進展に期待したいと思います。

実装に関しては、早速何人かによって実装例が出ているようです。自分でも使ってみて、より理解を深めていきたいと思います。
github.com
github.com
github.com

*1:この言い方が適切かは検討が必要

*2:この重み行列に関しては、どう学習するかの記載がないのですが、おそらく誤差逆伝搬で学習するのだと思います。

*3:適当なこと言っているかもしれません。

Rでスパースモデリング：Elastic Net回帰についてまとめてみる

R スパースモデリング

導入

回帰モデル構築の際、汎化性能を向上させるために正則化の手法がたびたび用いられます。これは、考えているデータ数に対して特徴量の数が非常に多い場合や、特徴量間に強い相関（多重共線性）がある場合に有効な方法となっています。このような場合に、通常の回帰モデル構築の際に用いられる2乗誤差などの目的関数に加え、L_pノルム（pは正整数）のような正則化項（もしくは罰則項）加えて最適化をおこなうことで先程の問題を解消することができます。こういった正則化項を加えた上でモデルの最適化をおこなう（ = パラメータを推定する）方法を、正則化法といいます。

代表的な正則化法に、Lasso, Ridge, Elastic Net回帰があります。これらは、解釈性も含めた特徴があり、必ずしも高精度のものだからよいわけではない、というのが私の考えです。しかし一方で、{caret}を使ってこの中で最も精度がよいものを採用しました、ということを行っている状況も（私の周りでは）見受けられます。精度向上だけが目的ならこういった立場でも良いのですが、Lasso回帰を始めとするスパースモデリングの強みの一つである、「人間の事前知識/解釈性」をモデルに取り入れることに関しては、必ずしも活かせないことになります。機械が自動で色々いい感じなものを作ってくれる未来はまだまだ先であり、モデリングの際に、どういったことが目的で、それをどう実現していくかをある程度理論的な背景を踏まえた上でおこなっていくことがまだまだ重要だと私は考えています。

まずは代表的な正則化法に関して整理しておきたいと考えたので、それらに関してまとめたものを備忘録的に載せておきます。

使用するデータセット

ボストン近郊の住宅価格のデータを利用します。Rでは{MASS}パッケージを導入すると付随してこのデータセットを使えるようになるため、{MASS}パッケージを利用します。

# ボストン近郊の住宅価格のデータを利用するため（だけ）に導入
if(!require(MASS)){
  install.packages("MASS", quiet = TRUE)
}
require(MASS)


> head(Boston)
     crim zn indus chas   nox    rm  age    dis rad tax ptratio  black lstat medv
1 0.00632 18  2.31    0 0.538 6.575 65.2 4.0900   1 296    15.3 396.90  4.98 24.0
2 0.02731  0  7.07    0 0.469 6.421 78.9 4.9671   2 242    17.8 396.90  9.14 21.6
3 0.02729  0  7.07    0 0.469 7.185 61.1 4.9671   2 242    17.8 392.83  4.03 34.7
4 0.03237  0  2.18    0 0.458 6.998 45.8 6.0622   3 222    18.7 394.63  2.94 33.4
5 0.06905  0  2.18    0 0.458 7.147 54.2 6.0622   3 222    18.7 396.90  5.33 36.2
6 0.02985  0  2.18    0 0.458 6.430 58.7 6.0622   3 222    18.7 394.12  5.21 28.7

目的変数はmedvで、説明変数候補はそれ以外を想定しています。具体的なモデル構築は、後ほどおこないます。

線形回帰モデル

以下のような線形回帰モデルを仮定します。
$$ \vec{y} = X\vec{\beta} + \vec{\epsilon} \tag{1}
$$
y,\ \vec{\beta},\ \vec{\epsilon}はそれぞれ目的変数、回帰係数（推定するパラメータ）、残差で、Xは計画行列（説明変数をまとめた行列）です。目的変数と特徴量は、それぞれ中心化・標準化されているとします。データ数n、特徴量の数pとすると、y,\ \vec{\epsilon}はn次元ベクトル、\vec{\beta}はp+1次元ベクトル（切片項も含む）、Xはn \times (p+1)行列となります。

回帰モデル構築の問題は、回帰係数\vec{\beta}を求める最適化問題へと帰着されます。最適化のためのよく用いられる目的関数は、以下のような2乗誤差関数です*1。
$$
S\left( \vec{\beta} \right) = \left( \vec{y} - X \vec{\beta} \right)^T \left( \vec{y} - X \vec{\beta} \right) \tag{2}
$$
この2乗誤差関数を最小にするようなパラメータ\vec{\hat{\beta}}は、実測とモデル式の誤差の2乗和を最小にするという意味で、最適なパラメータだと考えます。このパラメータは、目的関数をパラメータで微分したものを0とおいた方程式の解を求めればよく、簡単な計算で以下のようになることがわかります。
$$
\vec{\hat{\beta}} = \left( X^TX \right)^{-1} X^T \vec{y} \tag{3}
$$
式(3)の右辺は観測された量だけで構成されているため、それらを代入すれば回帰係数を求めることができます。

正則化法

先程の線形回帰モデルの議論は、特徴量とデータの関係によってはうまく機能しないことがあります。まず、どういった場合にどのような問題が生じるかを紹介し、それらをどのように解決していくか、という視点で正則化法の説明をしていきます。

多重共線性

式(3)で問題になるのは、多重共線性がある（特徴量間の相関が強い）場合です。

(X^TX)の逆行列を求めるためには、(X^TX)の行列式\text{det}(X^TX)を知る必要があります。しかし、多重共線性がある場合、(X^TX)のなかにほとんど同じ値を持つような列が複数出現することになります。線形代数などで行列式を求める計算を思い出すと、全く同じ値をもった列があると行列式が0になり、行列が特異（正則行列ではない）になっている状態となります。つまり、多重共線性がある場合は、\text{det}(X^TX)が非常に0に近くなります。

(X^TX)の逆行列は1 / \text{det}(X^TX)に比例しているため、\text{det}(X^TX)が0に近づくと逆行列(X^TX)^{-1}は無限大へ発散します。これは、 推定量の共分散\vec{\hat{\beta}} = \sigma ^2 (X^TX)^{-1}(\sigmaは残差が正規分布に従うとした場合の標準偏差)ということを思い出すと、推定量が非常に不安定な値を持つことを意味します。

Ridge回帰 (Hoerl and Kennard, 1970)

多重共線性の問題を回避する方法の一つが、正則化法です。Ridge回帰の場合は、L_2ノルムを加えたものを目的関数とします。
$$
S\left( \vec{\beta} \right) = \left( \vec{y} - X \vec{\beta} \right)^T \left( \vec{y} - X \vec{\beta} \right) + \lambda \vec{\beta}^T \vec{\beta} \tag{4}
$$
\lambda\ (\lambda \geq 0)は正則化の強さを制御する（ハイパー）パラメータです。通常の線形回帰の同様に、解を求めると以下のようになります。
$$
\vec{\hat{\beta} }_{\text{Ridge}} = \left( X^TX + \lambda \vec{1} \right) ^{-1} X^T \vec{y} \tag{5}
$$
\vec{1}は単位行列です。この単位行列（の\lambda倍）の行列の寄与のお陰で、(X^TX)ではほとんど同じ値を持つような列だったものがそうではなくなり、特異ではなくなります。そのため、多重共線性がある状況でも推定が可能になります。線形代数の言葉で言うと、正則化 = 正則行列化というわけです*2。

ただし、\lambdaの値が大きすぎると、推定量の共分散\vec{\hat{\beta}} = \sigma ^2 (X^TX)^{-1}は小さくなりますが、バイアス( (X^TX) / \lambda + \vec{1})^{-1} \vec{\beta}が大きくなるため、適切な\lambdaの調整は必要です。

Lasso回帰 (Tibshirani, 1996)

Ridge回帰によって、多重共線性の問題が回避できることがわかりました。しかし、Ridge回帰には、変数選択ができないという課題があります。式(5)から、大きな\lambdaをとることにより回帰係数全体が縮小される傾向があることがわかります。しかしながら、どれかの係数が完全に0になるといった性質は持っておらず、特徴量の数が多いときに解釈のし易い（特定の変数のみが寄与する）モデルが得ることは難しいという問題があります。

一方、変数選択はAICなどのモデル選択規準を用いて変数の追加・削除を行い最適な変数のセットを見つける問題です。こちらは、解釈性の高いモデル構築をできる可能性がありますが、多重共線性の問題がある場合は必ずしも安定な推定量が得られるわけではありません。

Lasso回帰は、Ridge回帰と変数選択の良いとこ取りをしたようなモデルになっています。この場合、L_1ノルムを加えたものを目的関数とします。
$$
S\left( \vec{\beta} \right) = \left( \vec{y} - X \vec{\beta} \right)^T \left( \vec{y} - X \vec{\beta} \right) + \lambda \sum _{j = 1}^p \left| \beta _j \right| \tag{6}
$$

式(6)は原点で不連続なため、通常の線形回帰のように厳密に解を求めることはできません。数値的に解く必要があります。数値計算の方法はいくつか種類があり、よく用いられる手法に座標降下法と呼ばれるものがあります。こういった何らかのアルゴリズムを用いて推定した結果を\vec{\hat{\beta}}_{\text{LASSO}}とします。
$$
\vec{\hat{\beta}}_{\text{LASSO}} = \text{argmin}_{\beta} \left[ \left( \vec{y} - X \vec{\beta} \right)^T \left( \vec{y} - X \vec{\beta} \right) + \lambda \sum _{j = 1}^p \left| \beta _j \right| \right] \tag{7}
$$

Lasso回帰は、パラメータ推定と変数選択を同時に行うことができ、スパースなモデルを構築することが可能です。特徴量が2つの場合の直感的なイメージ図は以下になります。正則化法は、制約条件付きの2乗誤差の最小化問題に置き換えることができます。ピンクの領域は、正則化項の大きさを固定した場合に許されるパラメータの領域となっています。最小2乗法による解がこのピンクの領域よりも外側にある場合、制約条件込みで目的関数を最小にするのは、最小2乗法による解を中心とした等高線とピンクの領域が交わる部分（図の星印）となります。Ridge回帰では、制約条件が円状であるため、回帰係数が全体的に小さくなる領域が解になりやすく、Lasso回帰では、尖っている部分（微分不可能な点で、特定の回帰係数の大きさが0となっている）が解になりやすくなります。そのため、Lasso回帰ではいくつかの係数が0となる解が推定されやすくなっています。
f:id:tekenuko:20171118170813j:plain

Lasso回帰の注意点

Lasso回帰は、変数選択の一致性が必ずしも保証されていないため、「正しい」変数選択が行われていない可能性があります。変数選択の一致性を担保したい場合は、Adaptive Lassoといった理論保証があるスパースモデリングの手法を使う必要があります。
tekenuko.hatenablog.com

Lasso回帰の欠点

Lasso回帰は、スパースなモデルを構築するためには非常に有用ですが、一方で以下のような欠点もあります。

  • データ数n, 特徴量の数をpとした場合に、p > nのときは高々n個の変数までしか選択できない
  • 相関の高い変数群がある場合、Lassoはその中の1つしか変数として選択できない

一つ目は、本当に重要な変数（0でないと推定したい変数）がnよりも多い場合に、重要な変数を選択しきれない、いう意味で問題となります。二つ目は、Grouping効果を考慮できないということを意味しています。遺伝子データのような場合、事前知識から似ている特徴量が複数あり、しかもそれらを変数として選択したい状況もあるかと思います。このような場合、Lasso回帰では選択される変数が似ている特徴量の中のどれか一つとなってしまいます。そうすると、モデル作成者が達成したい目的はLasso回帰では達成できなくなります。

Elastic Net回帰 (Zou and Hastie, 2005)

上記のようなLasso回帰の欠点を解決すべく考案されたものが、Elastic Net回帰です。Elastic Net回帰は、正則化項として、L_1ノルムとL_2ノルムの和を考えます。
$$
S\left( \vec{\beta} \right) = \left( \vec{y} - X \vec{\beta} \right)^T \left( \vec{y} - X \vec{\beta} \right) + \lambda \sum _{j = 1}^p \left\{ \alpha \left| \beta _j \right| + (1 - \alpha) \beta _j ^2 \right\} \tag{8}
$$
\lambda \ (\lambda \geq 0)は正則化項の大きさを制御するハイパーパラメータで、\alpha \ (0 \leq \alpha \leq 1)はL_1ノルムとL_2ノルムの相対的な寄与を調整するハイパーパラメータになります。\alpha = 0の場合がRidge、\alpha = 1の場合がLasso回帰に帰着します。

以下、Lasso回帰の欠点をElastic Net回帰がどのように解決しているかを見ていきます。

データ数n, 特徴量の数をpとした場合に、p > nのときは高々n個の変数までしか選択できない

こちらは、Elastic Net回帰の場合の推定量の計算を具体的に導出することでわかってきます。今、式(8)に登場する量たちを
$$
X^* = (1 + (1 - \alpha )\lambda) \begin{pmatrix}
X \\
\sqrt{(1 - \alpha) \lambda} \vec{1}_p \\
\end{pmatrix}, \ \ \
\vec{y}^* = \begin{pmatrix}
\vec{y} \\
\vec{0}_p \\
\end{pmatrix}, \\
\ \gamma = \alpha \lambda / \sqrt{1 + (1 - \alpha) \lambda} , \ \ \ \vec{\beta}^* = \sqrt{1 + (1 - \alpha) \lambda} \vec{\beta} \tag{9}
$$
とおくと、式(8)は
$$
S\left( \vec{\beta}^* \right) = \left( \vec{y}^* - X^* \vec{\beta}^* \right)^T \left( \vec{y}^* - X^* \vec{\beta}^* \right) + \gamma \sum _{j = 1}^p \left| \beta _j \right| \tag{10}
$$
とLasso回帰の形で書き直せます。そのため、式(10)の問題はLasso回帰の問題として解くことができ、その解を\vec{\hat{\beta}}^*とすると、Elasitc Net回帰に関する推定量は
$$
\vec{\hat{\beta }} _{\text{Elastic Net}} = \frac{1}{ \sqrt{1 + (1 - \alpha) \lambda} } \vec{\hat{\beta}}^* \tag{11}
$$
と求めることができます。今、X^*は(n + p)\times p行列となっているため、この行列のランクはpです。そのため、式(11)の推定量として、最高でpの成分が0でないと推定されます。これは、Lasso回帰のp > nのときは高々n個の変数までしか選択できない（0でない回帰係数の最大数はn）の欠点を解消するものになっています。

ここで、X^*というXよりもランクが大きくなりうる行列を定義していますが、これはRidge回帰の性質である疑似データ生成がもとになっています。つまるところ、Lasso回帰の欠点をRidge回帰の性質で補うという構造になっています。

相関の高い変数群がある場合、Lassoはその中の1つしか変数として選択できない

こちらは、原論文に証明があります。今\hat{\beta} _iをi番目のElastic Net回帰の推定量とし、ある(i, j)に関して\hat{\beta} _i \times \hat{\beta} _j > 0が成立しているとします。これは、これらの係数の符号が一致している状況になります。このとき、以下のような量を定義します。
$$
D(\alpha , \lambda) = \frac{1}{\sum _{i = 1}^n |y_i|} \left| \hat{\beta} _i -\hat{\beta} _j\right| \tag{12}
$$
詳しい導出は省略しますが、今考えている回帰係数に対応する特徴量間の相関係数を\rhoとすると、式(12)は以下のように評価することができます。
$$
D(\alpha , \lambda) \leq \frac{1}{(1 - \alpha) \lambda} \sqrt{2 (1 - \rho)} \tag{13}
$$
これは、\rho = 1（相関係数が1）の場合に\hat{\beta} _i = \hat{\beta} _j となることを意味しています。よって、Lasso回帰の場合と異なり、Elastic Net回帰では、相関の高い係数はどちらも0になるか、0にならないなら同じ値になる、といったGrouping効果を持つことがわかりました。

glmnetによる実験

以上のことから、それぞれの正則化法のおおざっぱな特徴は以下のようになります。

  • Ridge回帰：回帰係数全体が縮小推定される
  • Lasso回帰：相関の高い特徴量群がある場合、そのうちの一つが選択される（対応する回帰係数以外が0と推定される）
  • Elasitic Net回帰：相関の高い特徴量は、回帰係数が両方0になる、もしくは両方同じ値になる

これらの特徴を、ある程度恣意的な状況でモデルを構築して確かめてみることにします。使用データはボストン近郊の住宅価格のデータで、議論を簡単にするために変数をある程度絞って議論します。絞る材料とするために、いったんglmでモデルを構築し、stepwise法で変数選択をしてみます。

# glmでモデル作成
mod.full <- glm(medv ~., data = Boston)
# AICを基準にstepwise
mod.step <- stepAIC(mod.full, direction = "both", trace = 0)
# summaryを出力
summary(mod.step)

# 係数の部分だけ記載
Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  36.341145   5.067492   7.171 2.73e-12 ***
crim         -0.108413   0.032779  -3.307 0.001010 ** 
zn            0.045845   0.013523   3.390 0.000754 ***
chas          2.718716   0.854240   3.183 0.001551 ** 
nox         -17.376023   3.535243  -4.915 1.21e-06 ***
rm            3.801579   0.406316   9.356  < 2e-16 ***
dis          -1.492711   0.185731  -8.037 6.84e-15 ***
rad           0.299608   0.063402   4.726 3.00e-06 ***
tax          -0.011778   0.003372  -3.493 0.000521 ***
ptratio      -0.946525   0.129066  -7.334 9.24e-13 ***
black         0.009291   0.002674   3.475 0.000557 ***
lstat        -0.522553   0.047424 -11.019  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

結果を見ると、相対的にはrm, dis, ptratio, lstatの係数が有意であるようです。というわけで、これら4つの変数に絞り、さらにrmに対しては全く同じ変数のコピーを新たに加えたデータを作成します。

# rmのコピー
rm.dummy <- data.frame(rm_dummy = Boston$rm)
# new data.frame
Boston.new <- cbind(Boston[, c(6, 8, 11, 13, 14)], rm.dummy)

以下では、rmのコピー変数の回帰係数の解パスをモデルごとを見ていくことで、それぞれの正則化法の違いを見ていくことにします。その際に、glmnetに関する便利な補助ツールが幾つかあることが最近わかったので、活用していきます。具体的には、glmnetでもformula的に書くことができるようにするglmnetUtilsと、解パスをggplot2の形式で可視化してくれるggfortulyというものです。こちらに関しては、hoxo_mさんが最近紹介してくださりました。
qiita.com

Ridge回帰

先程恣意的に作成したデータで、Ridge回帰をし、解パスを見てみましょう。

# 必要なライブラリ
if(!require(glmnet)){
  install.packages("glmnet", quiet = TRUE)
}
require(glmnet)
require(glmnetUtils)
if(!require(githubinstall)){
  install.packages("githubinstall", quiet = TRUE) 
}
require(githubinstall)
if(!require("ggfortify")){
  githubinstall("ggfortify")
}
require(ggfortify)

# Ridge回帰（glmnetUtilsを併用）
Ridge <- glmnet(medv ~ ., data = Boston.new, alpha = 0)
# ggfortifyで可視化
autoplot(Ridge, xvar = "lambda")

f:id:tekenuko:20171118212000p:plain
（途中0を横切っているのもありますが…）正則化パラメータ\lambdaを大きくしていくと、係数の大きさが全体的に0に縮小していく傾向が見えます。また、rmとそのコピーrm_dummyはほぼほぼ同じような動きをしています。

Lasso回帰

Lasso回帰の場合にも、同じように解パスを見てみます。

# Lasso回帰（glmnetUtilsを併用）
Lasso <- glmnet(medv ~ ., data = Boston.new)
# ggfortifyで可視化
autoplot(Lasso, xvar = "lambda")

f:id:tekenuko:20171118212501p:plain
Ridge回帰の場合と比較し、rmとrm_dummyの振る舞いが明らかに違います。rm_dummyの回帰係数が常に0と推定されています。これは、Lasso回帰の「相関の高い特徴量群がある場合、そのうちの一つが選択される」という性質に対応しています。

Elastic Net回帰

# Elastic Net回帰（glmnetUtilsを併用）
ElasticNet <- glmnet(medv ~ ., data = Boston.new, alpha = 0.5)
# ggfortifyで可視化
autoplot(ElasticNet, xvar = "lambda")

f:id:tekenuko:20171118212916p:plain
Lasso回帰の欠点であった、Grouping効果が反映されています。少し見づらいですが、rmとrm_dummyの係数が0でなくなるタイミングが同じになっており、いったん0でないと係数された場合は、両者の回帰係数が似たような値になっています。

精度について

今回は主題ではないのであえて触れませんでしたが、実際に精度検証をしてみると、今回のデータではglm w/ stepwise > Elastic Net, Lasso > Ridgeの順で決定係数が大きかったです。例によってテストデータを含めた検証をしっかりやっているわけではないので、ここは参考程度で。実務の際はちゃんと汎化性能・解釈性などを踏まえて議論します。

まとめ

今回は、ある程度理論的な性質をもとに代表的な正則化法をまとめてみました。かなり恣意的な状況のデータではありましたが、相関が高い特徴量に対する実際の挙動の違いも確認しました。精度追求が要件の場合には今回の議論はあまり意味をなさないと思いますが、一方で、業務知識などである程度取り入れたい考えがあるときには、それに応じてモデルを構築するヒントの一助となるのではないかと思います。

*1:最尤法の枠組みで、正規分布に従う残差を仮定した場合でも、同じ目的関数となります。

*2:正則行列は、逆行列が存在するような正方行列のことです。行列式が0の場合、逆行列が存在しないのですが、正則化項を導入することで、逆行列が存在するような行列へと補正をかけています。

Rでスパースモデリング：Adaptive Lasso

R スパースモデリング

導入

スパース推定の代表的な手法として、Lassoがあります。様々なシーンで活用されているLassoですが、Lassoは変数選択の一致性が保証されないという欠点があります。Adaptive Lassoは、その欠点を補う形で提唱されている手法となっています。こちらは、ある条件のもとで変数選択の一致性が保証*1されており、数理統計学的により好ましい性質を持っています。

このAdaptive Lassoですが、Rでは{glmnet}以外のパッケージを使わないと簡単にできないとかなりの期間勘違いをしてました。そんな中、以下の記事を最近見かけまして、冷静に考えたら{glmnet}でも表現できるよなあと猛省した次第です。

RPubs - Adaptive LASSO Examples

以上の経緯から、挙動を確かめておこうという考えのもと、メモがてらAdaptive Lassoの紹介をしようと思います。

補足

上記の一致性の議論は、特徴量の数を固定して、データ数に対して無限大の極限を取った場合です。特徴量の数をデータ数よりも常に大きくとるようにした場合の極限の振る舞いも議論されており、例えば
http://www.keihirose.com/material/392-399_hirose.pdf
に載っております。

使用するデータセット

ボストン近郊の住宅価格のデータを利用します。Rでは{MASS}パッケージを導入すると付随してこのデータセットを使えるようになるため、{MASS}パッケージを利用します。

# ボストン近郊の住宅価格のデータを利用するため（だけ）に導入
if(!require(MASS)){
  install.packages("MASS", quiet = TRUE)
}
require(MASS)

# 目的変数、説明変数
y <- as.matrix(Boston[, 14])
X <- as.matrix(Boston[, -14])

目的変数はmedvで、説明変数はそれ以外です。また、{glmnet}にデータを投入する際は

  • 目的変数と説明変数を分ける
  • それぞれmatrixにする
  • 変数の中にfactorがあってはならない

といった制約があるので、それらを意識しています。

また、今回は予測に重きを置いているわけではなく、回帰係数の振る舞いに興味があるので、予測のために学習・検証用データに分けることはせず、全データを用いて推定を行います。

Lasso

以下のような回帰モデルを仮定します。
$$ \vec{y} = X\vec{\beta} + \vec{\epsilon}$$
y,\ \vec{\beta},\ \vec{\epsilon}はそれぞれ目的変数、回帰係数（推定するパラメータ）、残差で、Xは計画行列（説明変数をまとめた行列）です。データ数n、特徴量の数pとすると、y,\ \vec{\epsilon}はn次元ベクトル、\vec{\beta}はp+1次元ベクトル（切片項も含む）、Xはn \times (p+1)行列となります。

パラメータ推定をする際の目的関数は、二乗誤差を仮定します。Lasso(Least Absolute Shrinkage and Selection Operator)では、正則化項として L_1 ノルムを目的関数に加えます。
$$ L(\vec{\beta}) = \left\| \vec{y} - X \vec{\beta} \right\| ^2 + \lambda \| \vec{\beta} \|_1 $$
\lambdaは正則化項（もしくは罰則項）と呼ばれ、もとの二乗誤差に対して正則化の強さを制御するようなハイパーパラメータです。

上の式は原点で不連続なため、通常の線形回帰のように厳密に解を求めることはできません。数値的に解く必要があります。数値計算の方法はいくつか種類があり、よく用いられる手法に座標降下法と呼ばれるものがあります。こういった何らかのアルゴリズムを用いて推定した結果を\vec{\beta}_{\rm{Lasso}}とします。
$$ \vec{\beta}_{\rm{Lasso}} = \text{argmin}_\beta \left[ \left\| \vec{y} - X \vec{\beta} \right\| ^2 + \lambda \| \vec{\beta} \|_1 \right] $$


Lassoの特徴は、パラメータ推定と変数選択が同時にできることです。変数選択は、例えば相関の高い２つの変数があったとき、片方の変数の回帰係数が0と推定され、もう片方は0でない値となる、といったことが起きます。こういった状況のもと、推定結果が0でなかったものが変数として選択された、と考えます。この性質は、LassoがAICやBICといったモデル選択規準を用いてステップワイズ法を考える、といった変数選択のメカニズムが背後にあることに起因しています。こういった状況は、正則化項が離散的な関数になっていると読み取れるのですが、この項をうまく凸関数になるように連続極限をとった場合がLassoになります*2。

他の正則化項として代表的なものとしては、L_2ノルムを加えるRidge、L_1ノルムとL_2ノルムの線形結合を加えるElastic netなどがあります。これら正則化やアルゴリズムのより詳しい話は、例えば以下の記事などを参考としてください。
qiita.com

追記

argminの部分、投稿時はargmaxとタイポしてました。ご指摘いただいたynakahashiさんに感謝です！

Lassoの解パス

ハイパーパラメータである正則化項\lambdaを変化させると、推定結果も変わります。この変化の移り変わりを可視化したものを解パス（Solution Path）といいます。ここでは、ボストン近郊の住宅価格のデータに対してLassoを適用して、解パスがどうなるかを見てみます。

# モデリング
Lasso <- glmnet(x = X, y = y,
                alpha = 1)
# 正則化項を変化させたときの回帰係数の推移（解パス）
plt_res(Lasso)

f:id:tekenuko:20171102005446p:plain

ここで、plt_resはglmnet関数の出力をうまくggplot2で可視化する自作関数です。

# Library
if(!require(ggplot2)){
  install.packages("ggplot2", quiet = TRUE)
}
require(ggplot2)
if(!require(tidyr)){
  install.packages("tidyr", quiet = TRUE)
}
require(tidyr)

plt_res <- function(dgMatrix){

  # Convert to data.frame
  df_X <- as.data.frame(t(as.matrix(dgMatrix$beta)))
  df_loglambda <- dgMatrix$lambda
  df <- cbind(df_loglambda, df_X)
  # melt
  df_melt <- df %>%
    gather(key = df_loglambda, value = value)
  colnames(df_melt) <- c("lambda", "coefficient", "beta")
  # plot
  plt <- ggplot(df_melt) + 
    geom_line(aes(x = lambda, y = beta, group = coefficient, col = coefficient)) + 
    scale_x_log10()
  
  return(plt)
  
}

図を見ると、正則化項の寄与が小さい（\lambdaが小さい）ときは、0でない値に推定される回帰係数が多く、正則化項の寄与が大きくなると0と推定される係数が増えていくといった振る舞いになっています。このように、正則化項の寄与を変化させると、推定される係数も変化していきます。

回帰係数

上で解パスを見ましたが、ハイパーパラメータはどの値を取るのがよいでしょうか。上記の解パスの各\lambdaごとにRMSEなどが評価できるはずなので、その評価指標が最も良い点を選ぶ、というのも一つです。ここでは、より汎用的に評価するために、cross-validationを考えます。{glmnet}では、cv.glmnet関数を用いると簡潔に計算できます。

fit.Lasso.cv <- cv.glmnet(x = X, y = y,
                      nfolds = 10,
                      alpha = 1, 
                      standardize = TRUE)

nfoldはデータを10分割し、そのうちの一つをテストデータとする、といったサンプルを10パターン生成することを意味しています。alphaはL_1ノルムとL_2ノルムの相対的な寄与の大きさをコントロールしているパラメータでalpha=1のときがLasso、alpha=0のときがRidgeとなります。standardizeはモデリングの際にデータを標準化するかどうかのオプションです。

この結果、plot関数を用いると以下のように可視化されます。

plot(fit.Lasso.cv)

f:id:tekenuko:20171102010846p:plain
これは、\lambdaとRMSEの関係をプロットしたもので、エラーバーはデータ分割の仕方が起源として発生しています。この図を見ると、\lambdaは非常に小さい値が好まれるようです。

最もRMSEが小さい\lambdaの場合の推定結果は、以下になります。

coef(fit.Lasso.cv, s = fit.Lasso.cv$lambda.min)

# 出力
14 x 1 sparse Matrix of class "dgCMatrix"
                        1
(Intercept)  34.880894915
crim         -0.100714832
zn            0.042486737
indus         .          
chas          2.693903097
nox         -16.562664331
rm            3.851646315
age           .          
dis          -1.419168850
rad           0.263725830
tax          -0.010286456
ptratio      -0.933927773
black         0.009089735
lstat        -0.522521473

indusとageの係数が0と推定されています。

Adaptive Lasso

Adaptive Lassoは、L_1ノルムを目的関数に加える点はLassoと同じですが、重みが付く形になります。
$$ L(\vec{\beta}) = \left\| \vec{y} - X \vec{\beta} \right\| ^2 + \lambda \sum _{i = 1}^p \omega_i \left| \beta _i \right| $$
ここで、重みベクトル\vec{\omega} = (\omega _1, \cdots , \omega _p)は以下になります。
$$\vec{\omega} = 1 / \left|\vec{\hat{\beta}}\right|^\gamma $$
\vec{\hat{\beta}}はある一致推定量で、一致推定量の各成分の絶対値の\gammaの逆数が\vec{\omega}の各成分となっています。また\gamma > 0です。

一致推定量は、真の値との差がO(1/\sqrt{n})以下程度の精度が担保されるものなら何でもよいです。多くの場合、OLSの結果やRidgeの結果を使うようです。今回は、Ridge回帰の結果を用いることにします。
（2018-03追記 : Ridgeの結果を使うとオラクル性が満たされないかもしれません。調査中。）

Ridge回帰により何らかの一致推定量を得る

必ずしもcross-validationまでやる必要はありませんが、10-fold cross-validationにより、最もRMSEが小さくなる場合の回帰係数を取得します。

# Ridge回帰
fit.ridge.cv <- cv.glmnet(x = X, y = y,
                          type.measure = "mse",
                          alpha = 0, 
                          nfolds = 10, 
                          standardize = TRUE)
# 最もRMSEが小さくなる正則化項の場合の回帰係数
best_ridge_coef <- as.numeric(coef(fit.ridge.cv, s = fit.ridge.cv$lambda.min))[-1]

Adaptive Lassoの解パス

上で取得した係数を反映します。Adaptive Lassoは、glmnet関数のオプションpenalty.factorに1 / abs(best_ridge_coef))を代入することで実現できます。このオプションを認識していなかったので、glmnetでは簡単にAdaptive Lassoを書けないと思っていました。。解パスを表示すると、以下のようになります。

# モデリング
AdaLasso <- glmnet(x = X, y = y,
                  alpha = 1,
                  penalty.factor = 1 / abs(best_ridge_coef))
# 解パスを表示
plt_res(AdaLasso)

f:id:tekenuko:20171102013024p:plain

（2018-03追記 : 若干コードの見直しが必要かもしれません。調査中。）
線が上下している係数もあるので、実はあまり推定がうまくいっていないのかも、という懸念はありますが、Lassoの場合と比較して、だいぶ振る舞いが変わりました。どのタイミングでどの係数が0になるか、線の形状、色々変化しています。動く\lambdaの範囲は、実質的にRidgeの結果で割りこんだものを考えているので変化するのは理解できます。他の変化の仕方は明確に理由を説明するのは難しそうです。

回帰係数

Adaptive Lassoの場合も係数を表示しておきましょう。cross-validationした場合の図は省略します。

fit.AdaLasso.CV <- cv.glmnet(x = X, y = y,
                        type.measure = "mse",
                        nfolds = 10,
                        alpha = 1,
                        penalty.factor = 1 / abs(best_ridge_coef))
coef(fit.AdaLasso.CV, s = fit.AdaLasso.CV$lambda.min)

# 出力
14 x 1 sparse Matrix of class "dgCMatrix"
                        1
(Intercept)  38.501580556
crim         -0.098114529
zn            0.022165389
indus        -0.016969903
chas          3.129489627
nox         -20.469852957
rm            3.948669580
age           .          
dis          -1.345793859
rad           0.097441871
tax           .          
ptratio      -1.020675606
black         0.001601036
lstat        -0.546279678

0となる係数の組み合わせ、および係数の値が変化しています。このように、回帰係数のパターンもLassoと比較して変わるようです。

精度比較

精度が全てというわけではありませんが、LassoとAdaptive Lassoの両者で精度比較を行っておきます。評価指標はRMSEと決定係数R^2ですが、上述の通り、今回は全データを推定に使ったので、学習データに関するものの評価になっています*3。RMSEは{Metrics}のメソッドで計算し、決定係数R^2は予め関数を定義しておきます。

# 決定係数
r_squared <- function(y, ypred) {
  ybar <- mean(y)
  ## Total SS
  ss_tot <- sum((y - ybar)^2)
  ## Residual SS
  ss_res <- sum((y - ypred)^2)
  ## R^2 = 1 - ss_res/ ss_tot
  1 - (ss_res / ss_tot)
}

# LassoとAdaptive LassoそれぞれRMSEとR^2を計算
c("RMSE(Lasso) : ", round(rmse(y, pred_Lasso), 4))
c("R^2(Lasso) : ", round(r_squared(y, pred_Lasso), 4))
c("RMSE(Lasso) : ", round(rmse(y, pred_AdaLasso), 4))
c("R^2(Adaptive Lasso) : ", round(r_squared(y, pred_AdaLasso), 4))

# 出力
"RMSE(Lasso) : " "5.0299"   
"R^2(Lasso) : " "0.7003" 

"RMSE(Adaptive Lasso) : " "5.0435"
"R^2(Adaptive Lasso) : " "0.6987"

Adaptive Lassoの方がRMSEが大きく、決定係数が小さいという結果になってしまいました。変数選択をより正確にしたことの代償なのか…。今回はテストデータも含めて検証をしておりませんし、何よりデータに依存する話かもしれないので、ここの比較結果はあくまで参考程度にお願いします。

まとめ

今回は、数理統計学的に性質のよいとされるAdaptive Lassoのglmnetでの実装例を紹介しました。今まで壮大に勘違いをしていたのですが、案外シンプルにglmnetで書けることがわかったので、変数選択の一致性を気にする場合は積極的に活用していこうと思います。

*1:他にも推定量が漸近正規性をもつという性質も合わせて、オラクルプロパティを持つ、といいます。

*2:このあたりの議論は、統計数理研究所の公開講座「スパース推定」でされております。私はこの話を聴いたとき非常に感銘をうけました。

*3:実務接続を意識して比較する場合は、予測に関する評価もきちんと行わなければなりません。