トポロジカルデータアナリシス:ホモロジー群の紹介のための準備
導入
不定期でトポロジカルデータアナリシス(TDA)に関する紹介をします。今回は、図形の「穴」を数学的に表現するための準備をします。具体的に表現していくのは次回以降になります。
振り返り
これまで、データから図形を見立てる方法を紹介してきました。
tekenuko.hatenablog.com
tekenuko.hatenablog.com
これまでの話では、見立てた図形から情報を抽出する方法を紹介していませんでした。ここでは、図形の「穴」に着目するという考えを採用します。この「穴」に着目するという考えを数学的に表現するもの(の一つ)がホモロジー群です。
図形の穴を表現する方法は他にもあり、例えば、ホモトピー群というものがあります。これも図形の形や穴の数を反映するような量になっています。理論物理学ではホモトピー群のほうがよく応用に使われ、例えば液晶や渦、宇宙ひもやドメインウォール*1の分類や、非線形微分方程式の特解(ソリトン解)の分類などの応用があります。ただし、ホモトピー群はホモロジー群に比べて具体的に計算することは非常に難しく、計算機などに載せた応用には向いていません。そのため、上記のような具体的な図形の分類の問題ではホモロジー群がよく用いられます。
以下では、「穴」を数学的に表現するための準備的な考え方を紹介していきます。
穴は「境界」で特徴づけられる
今回、1単体(= 辺)の集まりで穴を作る例と作らない例を見ることで、穴を数学的に表現する手がかりを得られないかを考えていきます。ここで、単体とは、点(0次元)や辺(1次元)、三角形(2次元)、四面体(3次元)といった図形を一般化したものです。これらをそれぞれ0次元三角形、1次元三角形、...と呼ぶことにします。これは、次元空間内の
次元三角形という拡張ができます。この
次元三角形を
単体といいます。単体、およびそれを集めた単体的複体に関しては、ざっくり以下の記事でも紹介しています。
以下、1単体の集まりで穴を作る例(左)と作らない例(右)です。
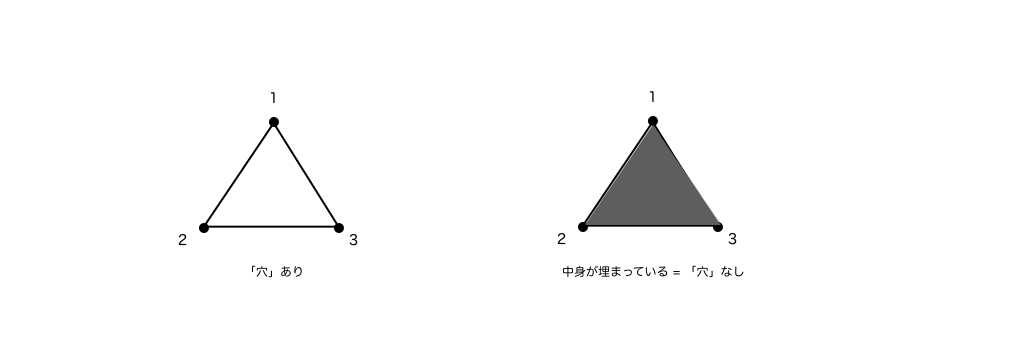
まず、左図は直感的にも穴が空いていそうですが、それはおそらく「端っこがない」ように見えるからだと思います。この「端っこ」は、数学的には「境界」と呼ばれます。例えば、頂点1と2からなる1単体の境界(端っこ)は頂点1と2です。しかしながら、頂点1と2には別の1単体(頂点1と3、および2と3からなる1単体)がくっついています。これは頂点1と3、および2と3からなる1単体に関しても同様です。つまり、これら3つの1単体の集まりには境界がありません。
一方で、右図は直感的には穴が空いていなそうです。ただし、1単体の集まりだけに着目すると、左図と構造は同じです。では、なぜ穴が空いていなそうと思うのでしょうか。
それは、1単体の中身を埋めるように2単体(三角形)が存在しているからです。これは、2単体の「端っこ」が1単体の集まりになっているとも言いかえられます。つまり、1単体の集まりに着目すると端っこを持っていませんが、この1単体の集まりは2単体の端っこになっています。
以上のことから、1単体に関しては穴を持つ条件は以下になりそうです。
「境界(端っこ)を持たない1単体の集まりで、2単体の集まりの境界になっていないもの」
つまり、ある次元の単体が与えられたとき、「境界」というものに着目すると穴による特徴づけが行なえそうです。実際、上の1単体の例を数学的に表現したものが1次ホモロジー群となっています。また、ここでの類推から、1単体を単体、2単体を
単体とすれば
次ホモロジー群という拡張も行えるのではないかと期待されます。
さらに数学的に定式化するために
今回は、図形の穴の分類において、「境界」というものに着目していけば良さそうであることを説明しました。次回以降、境界の数学的な表現方法を紹介していきます。ただし、そのためには単体などに関する表記や向きなどをきちんと定義した上で進める必要がある(というよりこれらを数式で表現しないと逆にわかりづらくなる)ので、以前の記事よりも若干かっちり定式化しつつ進めていきたいと思っています。
*1:これらはざっくりいうと、初期宇宙で対称性の破れによってできた一次元、二次元的な欠陥のようなものです。