多重共線性があるときにL2正則化項を加えると解けるようになることのざっくりとした説明
動機
回帰モデル構築の際、特徴量とデータの関係によってはうまく機能しない(解けない)ことがあります。たとえば、考えているデータ数に対して特徴量の数が非常に多い場合や、特徴量間に強い相関(多重共線性)がある場合です。このような場合に、正則化項と呼ばれる項を通常の回帰モデル構築の際に用いられる2乗誤差などの目的関数に加えることで、先程の問題を解消することができます。こういった正則化項を加えた上でモデルの最適化をおこなう( = パラメータを推定する)方法を、正則化法といいます。
上記の解けない場合が正則化によってどうして解けるようになるのか、数式で説明している資料があまりないと思ったので、メモとして残しておこうと思います。厳密でない部分もありますが、線形代数をそれなりに知っていればわかった気にはなれるかな、という感じの説明です。
記法と準備
データ数を, 説明変数の数を
, 計画行列を
, 正則化パラメータを
とします。
今回は、以下のような線形回帰モデルを仮定します。
$$ \vec{y} = X\vec{\beta} + \vec{\epsilon} \tag{1} $$
ここで、はそれぞれ目的変数、回帰係数(推定するパラメータ)、残差を表しています。
は
次元ベクトル、
は
次元ベクトル(切片項も含む)、
は
行列となります。
回帰モデル構築の問題は、回帰係数を求める最適化問題へと帰着されます。最適化のためのよく用いられる目的関数は、以下のような2乗誤差関数です。
$$
S( \vec{\beta} ) = ( \vec{y} - X \vec{\beta} )^T ( \vec{y} - X \vec{\beta} ) \tag{2}
$$
この2乗誤差関数を最小にするようなパラメータは、実測とモデル式の誤差の2乗和を最小にするという意味で、最適なパラメータだと考えます。このパラメータは、目的関数をパラメータで微分したものを0とおいた方程式の解を求めればよく、以下のようになることがわかります。
$$
\vec{\hat{\beta}} = ( X^TX )^{-1} X^T \vec{y} \tag{3}
$$
式(3)の右辺は観測された量だけで構成されているため、それらを代入すれば回帰係数を求めることができます。
式(3)が解けない場合の一つに、の逆行列が求められない場合があります。例えば、多重共線性がある場合、
のなかにほとんど同じ値を持つような列が複数出現することになります。全く同じ値をもった列があると行列式が0になることが知られており、行列式の割り算を含む逆行列は発散してしまいます。つまり、逆行列が求められない状況になります。このような行列を特異(正則行列ではない)であるといいます。
以下では、が特異である場合に正則化項、特に
ノルムを加えると式(3) (を拡張したもの) が解けるようになること、つまり推定量が存在することを説明します。
ノルムを考える理由は、手計算ができるからです*1。
簡単な説明
ノルムを加えた場合の目的関数は、以下のようになります。
(本によってファクターが微妙に違いますが、結果に影響はないので一番すっきりしたものにします。)
$$
S( \vec{\beta} ) = ( \vec{y} - X \vec{\beta} )^T ( \vec{y} - X \vec{\beta} ) + \lambda \vec{\beta}^T \vec{\beta} \tag{4}
$$
式(2)から式(3)への変形と同様に、式(4)の目的関数を最小とするパラメータを求めると、以下のようになります。
$$
\vec{\hat{\beta} }_{\text{Ridge}} = ( X^TX + \lambda \vec{1} ) ^{-1} X^T \vec{y} \tag{5}
$$
ここで、は単位行列です。逆行列
が存在することを示すことが目標です。
まず、は
の実対称行列である*2ため、直交行列*3によって対角化することができます。対角化された行列を
(
は
の固有値) とすると、
の逆行列は
$$
(X^T X)^{−1} = (PΓP^T )^{−1} = PΓ^{−1}PT
= P\text{diag} (1/\gamma _1, · · · , 1/\gamma _p)P^T \tag{6}
$$
となります。
ここで、行列が特異な場合にはいくつかのでゼロ固有値が出現しますが、その際は対応する
をいったん0でない値にしておき、あとで0の極限をとる、といった操作をするものと理解してください。式(6)から、特異な場合はある
に関して
となり、
の逆行列が発散してしまうため、最小二乗推定量が求まらなくなります。
次に、上記の直行行列を用いて逆行列
を変形してみましょう。
は単位行列であることから
$$
(X^TX + \lambda \vec{1})^{−1} = (P \Gamma P^T + \lambda \vec{1})^{−1}
= \{P(\Gamma + \lambda \vec{1})P^T \}^{−1}
= P(\Gamma + \lambda \vec{1})^{-1}P^T
$$
と変形できます。の対角成分は
であるため、逆行列は
$$
(X^TX + \lambda \vec{1})^{−1} = P\text{diag}(1/(\gamma _1 + \lambda), · · · , 1/(\gamma _p + \lambda))P^T
$$
となります。これより、が0でなければ
の極限でも
は無限大になりません。
よって、逆行列が存在するため、
は正則になり、推定量が求まります。
Ubuntu16.04LTSにSparkを入れる
そろそろSpark弱者を抜け出したい。
経緯
データ処理や分析の一つの手段として、Sparkをある程度できるようにしたい、と思ってはいるのですが、なんだかんだ腰を据えて…という感じになかなかならない日々が続いていました。おかげさまであんまり使いこなせてない状況なんですが、そろそろいい加減弱者でいるのもアレなので、自宅の環境でもラフに試せるような状況にしてしれっとできるようになってる状態を目指したいと思います。
Sparkのインストール
今回、私の環境とインストールするSparkのVersionは以下です。
- Ubuntu 16.04 LTS
- Spark 2.3.0
JDKのインストール
JDKは、Java Development Kitの頭文字を取ったもので、Javaによるプログラミングで必要なものが一式揃ったパッケージみたいなものです。
$ sudo apt-get install -y openjdk-8-jdk
Sparkのインストール
Sparkのダウンロードサイトから、入れたいVersionを指定してインストールすればよいです。
Downloads | Apache Spark
私は2.3.0を入れました。直接サイトからダウンロードするでもよいですが、コマンドラインからだと以下のような手順で行います。wgetでダウンロードして、解凍して実行しているだけです。SparkのHomeは/usr/local/sparkに指定しておきます(ここはお好み)。
$ wget http://ftp.riken.jp/net/apache/spark/spark-2.3.0/spark-2.3.0-bin-hadoop2.7.tgz $ tar zxvf spark-2.3.0-bin-hadoop2.7.tgz $ sudo mv spark-2.3.0-bin-hadoop2.7 /usr/local/ $ sudo ln -s /usr/local/spark-2.3.0-bin-hadoop2.7 /usr/local/spark
次に、コマンドラインでSparkを簡単に実行するために、.bashrcに以下の文言を追記します。
export SPARK_HOME=/usr/local/spark export PATH=$PATH:$SPARK_HOME/bin
ターミナルを再起動すれば、準備OKです。
Spark-shellの起動
実行すると、以下のような感じになります。

JupytetでPysparkを動かす
環境にもよりますが、.bashrcに以下の文言を追加すると私は大丈夫でした。
export PYSPARK_PYTHON=$PYENV_ROOT/shims/python #環境に合わせてパスを合わせること export PYSPARK_DRIVER_PYTHON=$PYENV_ROOT/shims/jupyter export PYSPARK_DRIVER_PYTHON_OPTS="notebook"
ターミナルを再起動して、pysparkとうったらjupyter notebookが開きます。
$ pyspark
ここから先はやっていきです。
Ubuntu 16.04LTSにTexを入れる
ちょっとした自分用メモです。
経緯
最近、個人でGPU環境などを持っておきたいと思って、自宅のPCを新調しました。そのついでにデュアルブートでUbuntu 16.04 LTSを入れ、そこで諸々環境を構築しています。それとは独立に最近、個人的な事情でTeX環境も整備しとく必要が出てきたのですが、今までLinuxでTeXの環境を作ったことがなかったので、ここにメモ書きとして残しておきます。
手順
なにはともあれ、apt-getをupgrade
sudoが必要かどうかは今までどういうセットアップしてきたかに依存すると思います。
$ sudo apt-get update $ sudo apt-get upgrade
エディタ
UbuntuでTeX Liveを使うときは何を使うとやりやすいかイマイチわかりません。私は何も設定していないとEmacsが起動するようになっていました。探してみると以下のページでKileというものを導入していたので、ここではそれを入れてみます。
www.kochi-struct-dynamics.rgr.jp
素直にapt-getでインストールします。
$ sudo apt-get install kile kile-l10n okular
Kileの設定
コマンドラインでkileと打つとKileが起動します。上部の設定からConfigure Kileを選択し、ツールのビルドにあるもののいくつかを変更します。
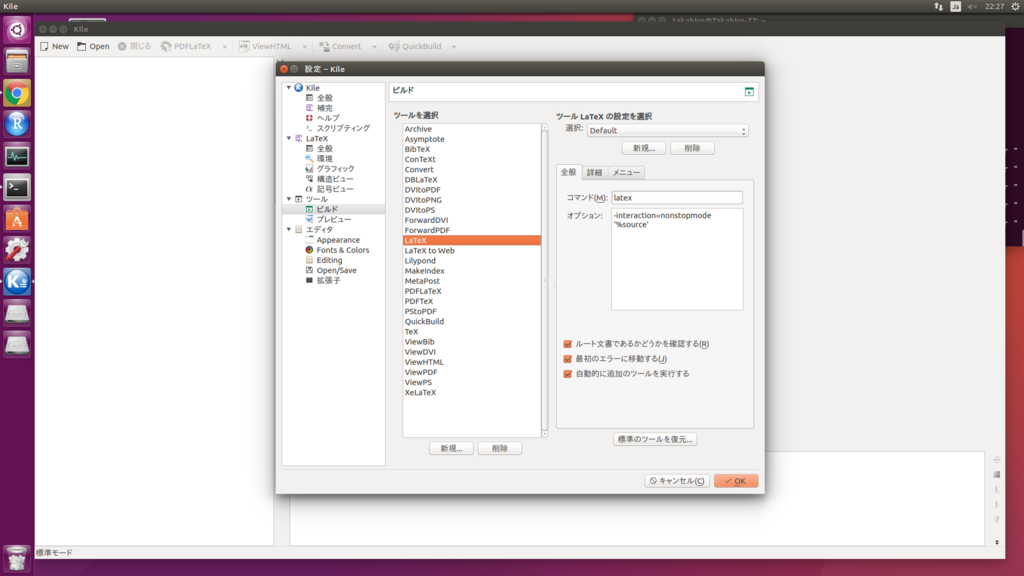
- DVItoPDF(デフォルトから変更しない)
- コマンド dvipdfmx
- オプション '%S.dvi'
- ForwordPDF(デフォルトから変更しない)
- コマンド okular
- オプション --unique '%absolute_target'
- BiBTeX
- コマンド pbibtex
- オプション '%S'
- QuickBuild
- ツールQuickBuildの設定を選択の部分がLaTeX+DVItoPDF+ForwordPDFとなるように下の全般の部分に適宜追加
これで、何かTeX fileを開いてQuickBuildすれば、TeX fileじたいに問題がなければコンパイルが通るはずです。エディタ周りは使いながら検討していきます。
NN論文の読み会でまた発表した
前回に続き、NN論文を肴に酒を飲む会で発表しました。
今回の論文のテーマは、強化学習でした。DQN周りの発展を勉強するいい機会だと思い、炎上ラーニング戦法で発表を申し込みました。私が選んだ論文は、Google DeepMindが昨年の10月に出した、DQN以降の深層強化学習のモデルをうまく融合させたモデルである「Rainbow」という論文です。
この論文のFigureがネタ的で趣深いので、興味あるかたはぜひ一読をおすすめします。論文のリンクは以下です。
[1710.02298] Rainbow: Combining Improvements in Deep Reinforcement Learning
ネタはさておき、論文投稿時点(2017年10月)でAtari2600というレトロゲームのスコアで最先端(State of The Art:SoTA)となっており、既存手法を圧倒する性能を獲得していました。
Rainbowもすごいのですが、現時点ではより性能のよいであろうモデルが提案されています。こちらもGoogle DeepMindから論文が出ており、Ape-Xと呼ばれるモデルになります。Rainbowで使われている手法の一部と、うまく並列処理する仕組みが組み合わされたもので、既存手法より効率的に学習することができるようです。最近までICLR 2018のreview中でしたが、acceptされたようです。
Distributed Prioritized Experience Replay | OpenReview
私の不勉強のため、発表しようと思っていた時点でこちらの論文を認識しておらず、結果として読み会はApe-Xの論文紹介で締めるというオチとなりました(笑)。かなりネタ的な発表だったかもと思いますが、個人的には最近の深層強化学習の発展を追う良い機会になりました。仕事ではDeep Learning関係を使っているわけではないので、こういう勉強して議論し合える機会は貴重だなと改めて感じました。今後も発表の機会があったら積極的にしていこうと思います。
PytorchでDeep Learning : CPU onlyでインストールする際のメモ
Deep Learningのフレームワークの一つにPytorchがあります。
Facebookを始めとして、様々な企業や大学が開発に携わっているようです。

PytorchはPython上でDeep Learningを行うためのフレームワークです。Preferred Networksが開発しているChainerからforkされた(らしい)ため、書き方や、ニューラルネットワークの構築をデータを流しながら行う*1といったChainerの特徴が引き継がれたものになっています。2017年の初頭に公開されたあとはどんどん人気を博していき、Tensorflow, Keras, Caffeに続くフレームワークとなっています。
Pytorchに興味をもったきっかけは、研究者の利用が多いことです。例えば、以下の柏野さんの資料などにそのような記載があります。
研究者の利用が多いということで、研究段階でPytorchを使ったり、調査の際にPytorchを使って実験するといった機会が多くなり、結果、Pytorch実装が早めに世に出やすくなると期待されます。ビジネス側でDeep Learningのキャッチアップを行っていきたいと考えたときに、Pytorchを知っておくと情報をいち早く得られるようになるのでは、と考えています。
というわけで、Pytorchについて調べてみようと思っています。
インストール
以下の例は、MacOS SierraでPython3.6(Anaconda利用)の場合です。Linuxで最初からGPUを利用できる環境を整えている場合はまた別の挙動になるのではと思います(未検証、GPU欲しい)。
雑にやりすぎで失敗した例
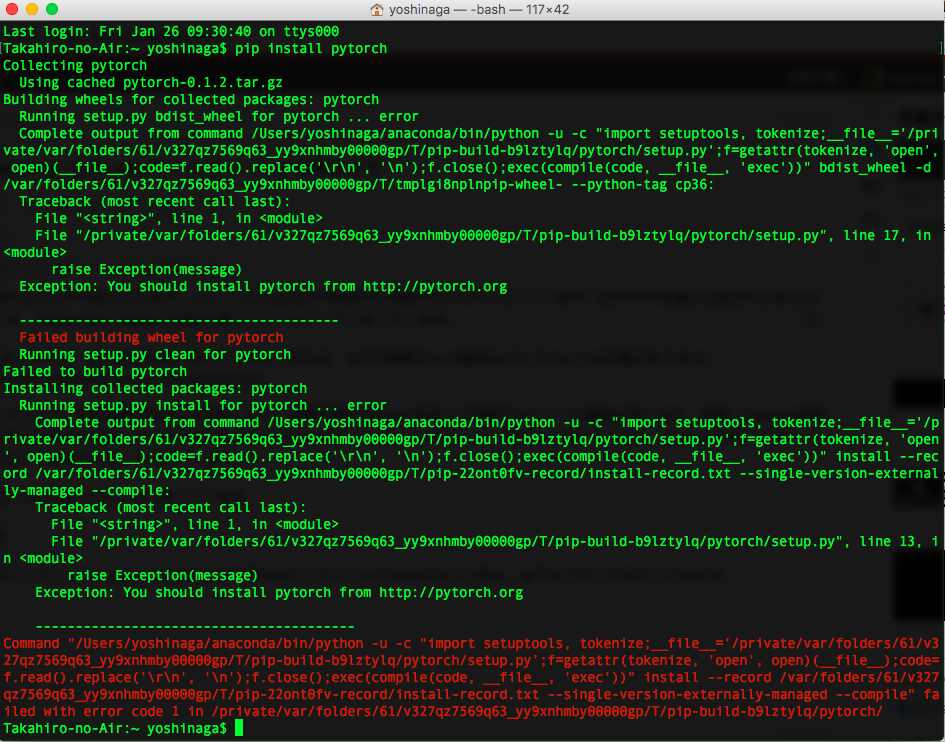
Pythonのフレームワークということで、pipなどでコマンドを叩けばインストールできるだろうと考え、以下のコマンドを打ってみます。
$ pip install pytorch
そうすると、私の環境では、以下のようなエラーが出たあと、Pytorchのページに飛ばされました。
そして、Get Startedの項目を見ると
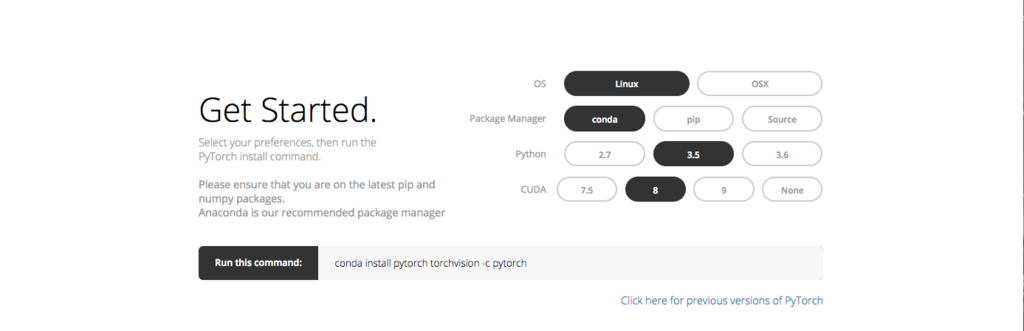
のように、OSやGPUあり/なしでコマンドを適宜変えないといけないらしいことがわかります。
環境に合わせてインストール
自分の環境に合わせてどうなるか見てみます。
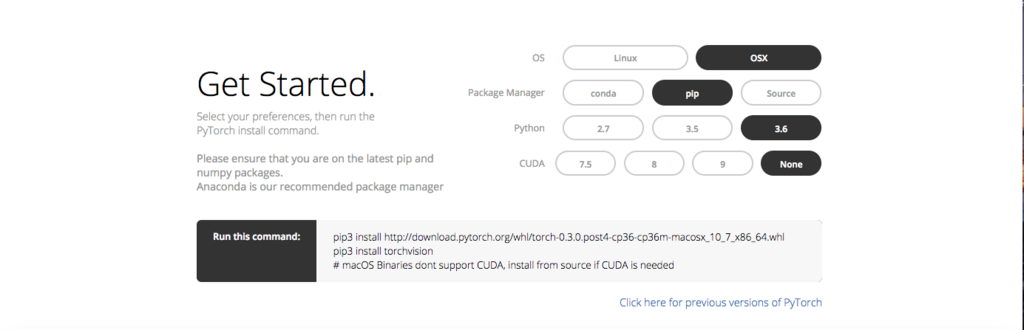
Anaconda入っているので、condaでも良い気がしますが、ここは好みで。CUDAとはNVIDIAが開発・提供している、GPU向けの汎用並列コンピューティングプラットフォームのことで、これが適切にインストール済みでないとNVDIAのGPUを使って計算することができません。自分の環境は、GPUに対応していないので、CPU onlyで使うためにCUDAの欄はNoneにしています。
(pip3とか推奨されているけど、pipでいいんじゃん?)
次に、推奨されたコマンド(pip3はpipに変えた)を打ってみます。
$ pip install http://download.pytorch.org/whl/torch-0.3.0.post4-cp36-cp36m-macosx_10_7_x86_64.whl $ pip install torchvision
結果、以下のようになり、インストールが成功します。
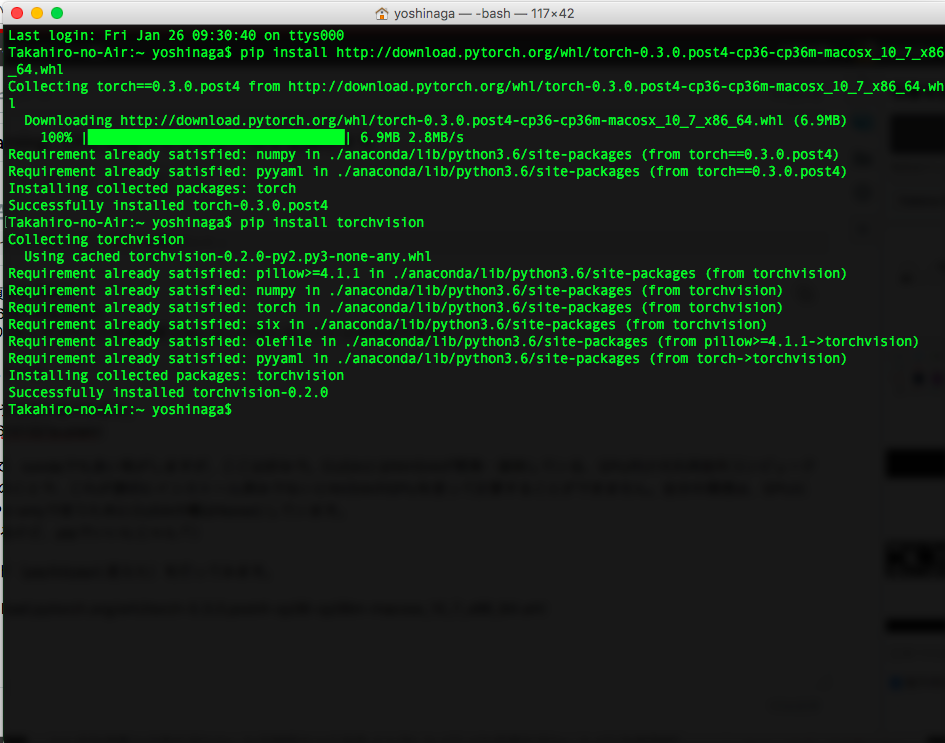
インストールした時期によってバージョンは多少変化すると思いますが、pip listで
torch (0.3.0.post4) torchvision (0.2.0)
というものが見れていればPythonでPytorchが使える状況になっていると思います。実際、ipythonあたりを雑に起動してみて
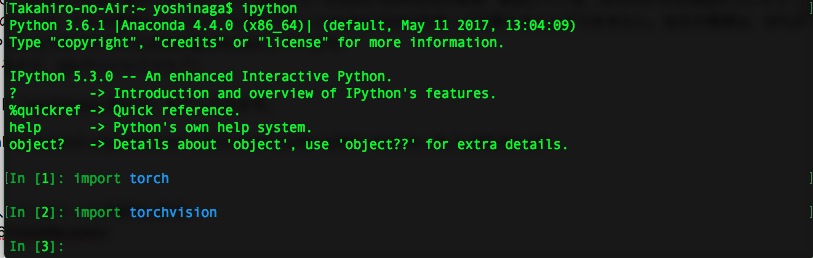
という感じで、問題なくimportできています。
Next Step
今回は、Pytorchのインストールについてのメモを紹介しました。雑にpip使っていきなりサイトに飛ばされてびっくりしたのですが、普通はサイトにいってインストール方法を読んでから実行しますよね。。単に自分のアホさを露呈しただけでした。
割りと趣味的な感じなので、ちまちまとやっていく感じにはなると思いますが、Pytorchを使って色々と試していきたいと思っています。仕事でDeep Learningをやる機会があったらPytorchを使ってみたいんですけどね。そういう機会があればいいなあ。
*1:Define by runという考え方です。このような設計にすると、ミニバッチごとに異なるネットワークを準備するなどが可能になります。