Pythonでデータ分析：線形回帰モデル - データサイエンティスト(仮)

導入

データ分析にて、最も基本的な回帰分析から始めていきます*1。回帰分析とは、説明したい変数（目的変数）とそれを説明するための変数（説明変数）の間の関係を求める手法です。機械学習の手法の区分としては、教師あり学習（解答に相当する教師データを用いてモデルを構築）に属するものです。

回帰分析の目的は大きく2種類あります。

理解：文字通り、変数間の構造・関係の理解
- 例：ある病気に対して、どのような遺伝子が寄与しているかをマイクロアレイデータなどのデータを用いて明らかにする
予測：変数間の関係をもとに、将来予測をする
- 例：過去の広告の投下量と売上実績から、これらの関係を説明するモデルを構築し、それをもとに将来の広告への投資計画を立てる

ビジネスの世界では、予測を目的に使用されることがほとんどです。それは、モデル構築によって要因を明らかにするだけでなく、その後の施策でそのモデルの知見を使い、価値を生み出すことが求められるからです。逆に、アカデミックでは理解が目的の研究も一定数あります。実務でデータ分析をやっている方は、例えば、マーケティングサイエンス学会に参加するとこのあたりの思想の違いを感じ取れて面白いと思います。

使用するデータセット

ボストン近郊の住宅情報のデータを使用します。こちらは、無償で提供されており、例えばUCI Machine Learning Repository(UCI Machine Learning Repository: Housing Data Set)からダウンロードすることが可能です。ここでは、scikit-learnからロードする形で導入します。

## 必要なライブラリのインポート
from pandas import DataFrame
from sklearn.datasets import load_boston

## データの用意
# ボストンデータをインポート
boston = load_boston()
# 説明変数たちをDataFrameへ変換
df = DataFrame(boston.data, columns = boston.feature_names)
# 目的変数をDataFrameへ追加
df['MEDV'] = np.array(boston.target)

DataFrameという形式で保持するために、pandasを導入しています。最初の数行を表示してみます。

# 最初の5行を表示
df.head()

# コンソールでの表示結果
>>> df.head()
      CRIM    ZN  INDUS  CHAS    NOX     RM   AGE     DIS  RAD    TAX  
0  0.00632  18.0   2.31   0.0  0.538  6.575  65.2  4.0900  1.0  296.0   
1  0.02731   0.0   7.07   0.0  0.469  6.421  78.9  4.9671  2.0  242.0   
2  0.02729   0.0   7.07   0.0  0.469  7.185  61.1  4.9671  2.0  242.0   
3  0.03237   0.0   2.18   0.0  0.458  6.998  45.8  6.0622  3.0  222.0   
4  0.06905   0.0   2.18   0.0  0.458  7.147  54.2  6.0622  3.0  222.0   

   PTRATIO       B  LSTAT  MEDV  
0     15.3  396.90   4.98  24.0  
1     17.8  396.90   9.14  21.6  
2     17.8  392.83   4.03  34.7  
3     18.7  394.63   2.94  33.4  
4     18.7  396.90   5.33  36.2

全部で14個のカラムがありますが、今回は最初の13個を説明変数、14個目を目的変数として使用することを想定しています。それぞれのカラムにある情報は以下です。

CRIM : 犯罪発生率（人口単位）
ZN : 25000平方フィート以上の住宅区間の割合
INDUS : 非小売業の土地面積の割合（人口単位）
CHAS : チャールズ川沿いかどうかフラグ（川沿いなら1、そうでなければ0）
NOX : 窒素感化物の濃度（pphm単位）
RM : 一戸あたりの平均部屋数
AGE : 1940年よりも前に建てられた家屋の割合
DIS : ボストンの主な5つの雇用圏までの重み付き距離
RAD : 幹線道路へのアクセス指数
TAX : 10000ドルあたりの所得税率
PTRATIO : 教師あたりの生徒の数（人口単位）
B : 1000(Bk - 0.63)^2として計算される量（Bkはアフリカ系アメリカ人居住者の割合（人口単位））
LSTAT : 低所得者の割合
MEDV : 住宅価格の中央値（単位は1000ドル）

線形回帰モデルの構築

通常はモデル構築に至るまでにデータ理解や基礎集計、データ加工といった非常に重要なステップがありますが、省略します。ここでは、目的変数をMEDV、説明変数をCRIM~LSTATとした回帰モデルを構築します。今回、目的変数は連続値とみなすことができるため、回帰モデルの中でも最も単純な、目的変数と説明変数間の関係が線形である場合を仮定します。
$MEDV \sim \beta _0 + \beta _1 \times ZN + \cdots + \beta _{13} \times LSTAT + \epsilon$
$\beta _0, \cdots ,\beta _{13}$ は回帰係数と呼ばれる量で、それぞれの変数がどれだけ目的変数に寄与するかを表しています。特に、 $\beta _0$ はすべての説明変数の寄与が0の場合も残る「ベース」的な量で、切片（Intercept）とも呼ばれます。 $\epsilon$ は残差と呼ばれる量で、各データとモデル式の「ズレ」を表します。線形回帰モデルでは、各データ点の残差の二乗を足し合わせたものを最小にするという条件のもとで、係数を求めます。

scikit-learnによる係数の推定

ここでは、いったん全データを用いて線形回帰モデルを構築（=回帰係数の推定）をします。scikit-learnにあるLinearRegressionを用いると、簡単に係数の推定が行えます。

## 説明変数と目的変数
# 説明変数
X = df.loc[:, boston.feature_names].values
# 目的変数
y = df.loc[:, 'MEDV'].values
## 必要なライブラリのインポート
from sklearn.linear_model import LinearRegression
# オブジェクト生成
mod = LinearRegression(fit_intercept = True, normalize = False, copy_X = True, n_jobs = 1)
# fit関数でパラメータ推定
mod.fit(X, y)

LinearRegressionの引数を明示的に書いてありますが、それぞれは以下の意味を持っています。

fit_intercept : 切片項をモデル式に入れるかどうか。デフォルト値はTrue。
normalize : 説明変数を正規化するかどうか。デフォルト値はFalse。
copy_X : メモリ内でデータを複製してから実行するかどうか。デフォルト値はTrue。
n_jobs : 計算に使うジョブ数。デフォルト値は1で-1にするとすべてのCPUを使って計算。

回帰係数を出力してみます。

# 回帰係数を出力
print(mod.coef_)
print(mod.intercept_)

# 出力結果
>>>print(mod.coef_)
[ -1.07170557e-01   4.63952195e-02   2.08602395e-02   2.68856140e+00
  -1.77957587e+01   3.80475246e+00   7.51061703e-04  -1.47575880e+00
   3.05655038e-01  -1.23293463e-02  -9.53463555e-01   9.39251272e-03
  -5.25466633e-01]
>>>print(mod.intercept_)
36.4911032804

学習データ、検証データに分割して性能評価

先程は、全データを用いて回帰係数の推定を行いました。しかし、それだけだと今持っているデータ「だけ」によく当てはまるモデルを作ってしまい、予測で良い性能を発揮しない場合があります。それを確認するための方法として、パラメータ推定の際に使用しなかったデータを用いて精度検証を行う、という方法があります。ここでは、持っているデータを学習用、検証用の2種類に分割して精度検証します。

上記のような精度検証は、scikit-learnを利用すると簡単に行うことができます。

# train_test_splitをインポート
from sklearn.cross_validation import train_test_split
# 70%を学習用、30%を検証用データにするよう分割
X_train, X_test, y_train, y_test = train_test_split(X, y, 
test_size = 0.3, random_state = 666)
# 学習用データでパラメータ推定
mod.fit(X_train, y_train)
# 作成したモデルから予測（学習用、検証用モデル使用）
y_train_pred = mod.predict(X_train)
y_test_pred = mod.predict(X_test)

残差プロット

モデルの性能を見る大雑把な方法として、残差プロットがあります。これは、予測値と実際の観測値の差分を可視化し、モデルで拾いきれていない非線形性や外れ値がないか、といった観点から、残差がランダムに分布しているかをチェックする方法です。数値的に性能を評価する前に、可視化して傾向を見ておくのは重要です。残差をプロットするコードは、例えば以下になります。

# matplotlibをインポート
import matplotlib.pyplot as plt
# Jupyterを利用していたら、以下のおまじないを書くとnotebook上に図が表示
%matplotlib inline
# 学習用、検証用それぞれで残差をプロット
plt.scatter(y_train_pred, y_train_pred - y_train, c = 'blue', marker = 'o', label = 'Train Data')
plt.scatter(y_test_pred, y_test_pred - y_test, c = 'lightgreen', marker = 's', label = 'Test Data')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
# 凡例を左上に表示
plt.legend(loc = 'upper left')
# y = 0に直線を引く
plt.hlines(y = 0, xmin = -10, xmax = 50, lw = 2, color = 'red')
plt.xlim([10, 50])
plt.show()

コードの実行結果は以下のようになります。
f:id:tekenuko:20160919144249p:plain

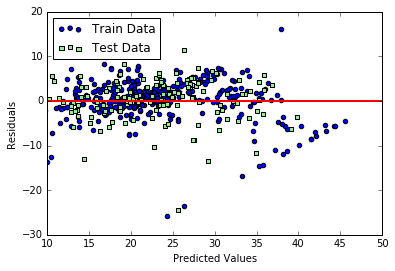
予測が完璧である場合は、残差はちょうど0になりますが、現実的にはそれはまずありません。良い回帰モデルの場合は、残差がちょうと0を中心にランダムに分布するような傾向が見えるはずです。今回のモデルに関しては、概ねランダムに分布しているようにも見えますが、学習用データを使った場合の残差に関してグラフの右下になにか直線的な傾向があり、モデルに取り切れていない情報がある可能性があります。

平均二乗誤差、決定係数

数値的にモデルの性能を評価する指標の例として、平均二乗誤差（Mean Squared Error : MSE）や決定係数（ $R^2$ ）があります。これらは、データ点を $i$ でラベル付けしたとすると、以下のように定義されるものです。
$MSE = \frac{1}{n} \sum _{i = 1}^n (y^{(i)} - y_{pred}^{(i)})^2$
$R^2 = 1 - \frac{MSE}{Var(y)}$
MSEは、誤差の二乗和の平均値で、学習用データ、検証用データともに小さければモデルの性能が良い、と判断されます。 $R^2$ に関しては、MSEが0の場合に1をとる、つまりモデルの性能が良いほど1に近い量になります。また、 $R^2$ は学習用データに関しては0から1の値を取りますが、検証用データの場合には負の値を取ることもあります。

MSEと $R^2$ は、scikit-learnを用いると簡単に評価できます。これらを出力するコードは、以下のようになります。

# 平均二乗誤差を評価するためのメソッドを呼び出し
from sklearn.metrics import mean_squared_error
# 学習用、検証用データに関して平均二乗誤差を出力
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 学習用、検証用データに関してR^2を出力
print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_train, y_train), mod.score(X_test, y_test)))

# 出力結果
>>>print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
MSE Train : 21.371, Test : 24.336
>>>print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_train, y_train), mod.score(X_test, y_test)))
R^2 Train : 0.763, Test : 0.659