Pythonでデータ分析:非線形効果を導入
導入
前回、ボストン近郊の住宅情報のデータを用いて線形回帰モデルを作りました。
tekenuko.hatenablog.com
今回は、モデルの性能を上げる可能性の一つとして、多項式や指数・対数などの非線形効果をモデルに投入した場合の振る舞いを見ようと思います。
使用するデータセット
前回と同様、ボストン近郊の住宅情報のデータを使用します。
# 必要なライブラリのインポート import numpy as np import pandas as pd from pandas import DataFrame from sklearn.datasets import load_boston # データのロード、マージ boston = load_boston() df = DataFrame(boston.data, columns = boston.feature_names) df['MEDV'] = np.array(boston.target)
非線形効果を入れる前に
非線形効果を入れる際に、(私個人の考えとして)注意する点が2つあります。
- 過学習
- 投入コスト
過学習に関しては、モデルの複雑さが増すことから生じます。一般に、説明変数と目的変数のデータがそれぞれn個あったとすると、n-1次の多項式を用いると残差が0で説明できてしまいます。しかしながら、このようなモデルは今のデータセットのみに強く適合するものであり、新しいデータに対する説明力が極端に低くなってしまいます。そのため、常に学習データと検証データにおける精度のバランスを見ながらモデルを評価する必要があります。
投入コストに関しては、ビジネスでのデータ分析の場面で度々考慮しなければならない問題です。実務では、納期と精度、そして費用対効果のバランスをうまくとることが求められます。非常に時間をかけて(ほんのすこし精度が向上する)非線形効果を取り入れたモデルを構築するよりも、時間をかけずに単純な(ある程度精度が担保された)モデルを作成し、早く実運用に載せて知見をためるという方が案件状況によっては良い場合があります。そのため、モデルの複雑化に関しては、要件定義や分析設計の段階でプロジェクト内での認識合わせが非常に重要になります*1。
このような注意点があるため、闇雲に変数を複雑化することはできるだけ避けたほうがよいというのが私個人の考えです。検討する場合も、事前知識を援用して判断できるもののみを考え、複雑化は最小限に留める、などします*2。
可視化
事前知識を援用する方法の一つに、データを可視化するという方法があります(あると思っています)。以下のように、変数間でどのような関係が見られるかをプロットしてみます。
# matplotlib(のなかのpyplot)をインポート import matplotlib.pyplot as plt # seaborn(可視化の補助を行う)のインポート import seaborn as sns # Jupyterを利用していたら、以下のおまじないを書くとnotebook上に図が表示 %matplotlib inline # グラフのスタイルを指定 sns.set(style = 'whitegrid', context = 'notebook') # 変数のペアの関係をプロット sns.pairplot(df, size = 2.5) plt.show()
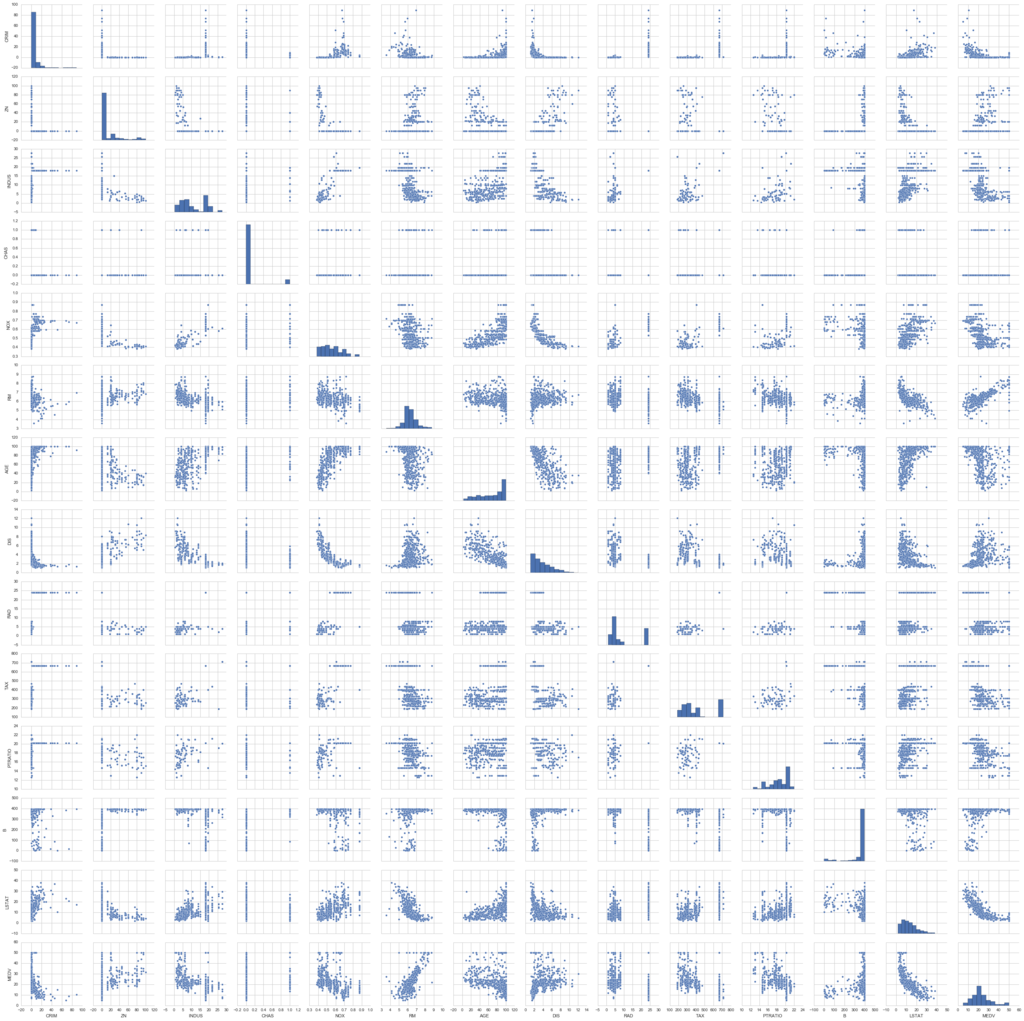
今回は、説明変数と目的変数の関係、つまり図の一番下(もしくは一番右)に着目します。
とはいえ、これでは変数が多すぎて情報過多になっています(汗)。そのため、今回フォーカスしたい部分に制限した図を以下に表示します。
# カラムを制限してプロット sns.pairplot(df[['LSTAT', 'MEDV']], size = 2.5) plt.show()
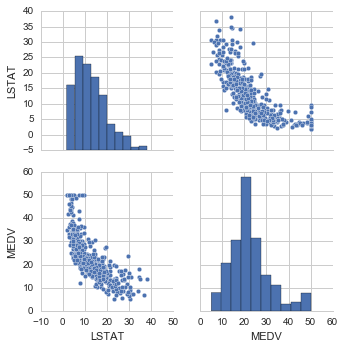
このLSTATとMEDVの散布図を見ると、直線的というよりは若干曲線的な関係性がありそうです。そのため、LSTATに関して非線形効果を導入することがモデルの性能向上に役に立つかもしれません。今回は、単純化したい理由で、説明変数はLSTATのみに絞り、モデルに投入する式を変えた場合の精度の変化を見たいと思います。
非線形効果 : 多項式
線形(1次)からの素朴な拡張として、多項式効果を入れる、という方法があります。ここでは、2次(quadratic)と3次(cubic)の項をモデルに投入した場合の精度を評価してみます。
多項式項を追加する場合、モデル構築の大枠は変更しなくても大丈夫です。
# 説明変数 X = df.loc[:, ['LSTAT']].values # 目的変数 y = df.loc[:, 'MEDV'].values # モデルのインスタンス生成 from sklearn.linear_model import LinearRegression mod = LinearRegression()
変更を受けるのは、変数加工の部分です。つまり、自分で2次、3次の変数を作成し、それを代入する、ということが実際にやることです。幸い(?)、scikit-learnには非線形の変数を加工する機能がありますので、ここではそれを利用します。
多項式の変数加工は、以下のメソッドを呼び出すことで行えます。
from sklearn.preprocessing import PolynomialFeatures # 2次(までの)変数を作成するインスタンス quadratic = PolynomialFeatures(degree = 2) # 3次(までの)変数を作成するインスタンス cubic = PolynomialFeatures(degree = 3) # 変数作成 X_quad = quadratic.fit_transform(X) X_cubic = cubic.fit_transform(X)
これで多項式変数の作成ができました。
次に、線形回帰モデル、2次の項を追加、3次の項まで追加したモデルを作成します。
# モデル式用に変数を作成 X_fit = np.arange(X.min(), X.max(), 1)[:, np.newaxis] # 線形回帰モデル、予測値、R^2を評価 mod_lin = mod.fit(X, y) y_lin_fit = mod_lin.predict(X_fit) r2_lin = mod.score(X, y) # 2次の項を追加、予測値、R^2を評価 mod_quad = mod.fit(X_quad, y) y_quad_fit = mod_quad.predict(quadratic.fit_transform(X_fit)) r2_quad = mod.score(X_quad, y) # 3次の項を追加、予測値、R^2を評価 mod_cubic = mod.fit(X_cubic, y) y_cubic_fit = mod_cubic.predict(cubic.fit_transform(X_fit)) r2_cubic = mod.score(X_cubic, y)
各モデルの結果をプロットします。参考のため、モデル式も重ねてプロットします。
# データ点をプロット plt.scatter(X, y, label = 'Traning points', color = 'lightgray') # 線形モデルのモデル式 plt.plot(X_fit, y_lin_fit, label = 'linear (d = 1), $R^2=%.2f$' % r2_lin, color = 'blue', lw = 2, linestyle = ':') # 2次 plt.plot(X_fit, y_quad_fit, label = 'quadratic (d = 2), $R^2=%.2f$' % r2_quad, color = 'red', lw = 2, linestyle = '-') # 3次 plt.plot(X_fit, y_cubic_fit, label = 'cubic (d = 3), $R^2=%.2f$' % r2_cubic, color = 'green', lw = 2, linestyle = '--') plt.xlabel('LSTAT') plt.ylabel('MEDV') plt.legend(loc = 'upper right') plt.show()
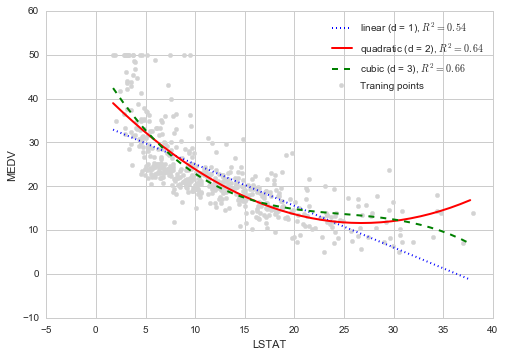
結果を見ると、3次の項まで追加した場合が最も当てはまりのよいモデルになっていることがわかります。
学習用データと検証用データで分割
前回の精度検証と同様、今回も学習用データと検証用データに分割して性能を判断してみます。
# 必要なメソッドのインポート from sklearn.cross_validation import train_test_split # 学習用70%、検証用30%に分割 (X_train, X_test, y_train, y_test) = train_test_split(X, y ,test_size = 0.3, random_state = 666) (X_quad_train, X_quad_test, y_train, y_test) = train_test_split(X_quad, y , test_size = 0.3, random_state = 666) (X_cubic_train, X_cubic_test, y_train, y_test) = train_test_split(X_cubic, y , test_size = 0.3, random_state = 666)
それぞれのモデルでのMSEとは以下になります。
線形モデル
# モデル作成 mod.fit(X_train, y_train) y_train_pred = mod.predict(X_train) y_test_pred = mod.predict(X_test) # 必要なメソッドのインポート from sklearn.metrics import mean_squared_error # 学習用、検証用データに関して平均二乗誤差を出力 print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred))) # 学習用、検証用データに関してR^2を出力 print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_train, y_train), mod.score(X_test, y_test))) # 出力 >>>print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred))) MSE Train : 42.126, Test : 30.120 >>>print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_train, y_train), mod.score(X_test, y_test))) R^2 Train : 0.532, Test : 0.578
2次の項を追加
# モデル作成 mod.fit(X_train, y_train) y_train_pred = mod.predict(X_quad_train) y_test_pred = mod.predict(X_quad_test) # 必要なメソッドのインポート from sklearn.metrics import mean_squared_error # 学習用、検証用データに関して平均二乗誤差を出力 print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred))) # 学習用、検証用データに関してR^2を出力 print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_quad_train, y_train), mod.score(X_quad_test, y_test))) # 出力 >>>print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred))) MSE Train : 32.211, Test : 26.241 >>>print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_quad_train, y_train), mod.score(X_quad_test, y_test))) R^2 Train : 0.642, Test : 0.632
3次の項を追加
# モデル作成 mod.fit(X_train, y_train) y_train_pred = mod.predict(X_cubic_train) y_test_pred = mod.predict(X_cubic_test) # 必要なメソッドのインポート from sklearn.metrics import mean_squared_error # 学習用、検証用データに関して平均二乗誤差を出力 print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred))) # 学習用、検証用データに関してR^2を出力 print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_cubic_train, y_train), mod.score(X_cubic_test, y_test))) # 出力 >>>print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred))) MSE Train : 29.914, Test : 26.968 >>>print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_cubic_train, y_train), mod.score(X_cubic_test, y_test))) R^2 Train : 0.668, Test : 0.622
検証用データも含めて判断すると
という傾向があるように見えます。
他の非線形効果
多項式以外の投入方法として、指数、対数、平方根をとるといった方法があります。今回のデータだと、LSTATの対数をとり、MEDVの平方根をとる、という操作を行うとよりモデルの当てはまりがより向上します。結果をプロットすると以下のようになります。
# 非線形変換 X_log = np.log(X) y_sqrt = np.sqrt(y) # 線形回帰モデル作成、R^2計算 X_fit = np.arange(X_log.min(), X_log.max() + 1, 1)[:, np.newaxis] mod_log = mod.fit(X_log, y_sqrt) y_sqrt_fit = mod_log.predict(X_fit) r2_sqrt = mod.score(X_log, y_sqrt) # プロット plt.scatter(X_log, y_sqrt, label = 'Traning points', color = 'lightgray') plt.plot(X_fit, y_sqrt_fit, label = 'linear (d = 1), $R^2=%.2f$' % r2_sqrt, color = 'blue', lw = 2, linestyle = ':') plt.xlabel('log[LSTAT]') plt.ylabel('sqrt[MEDV]') plt.legend(loc = 'upper right') plt.show()
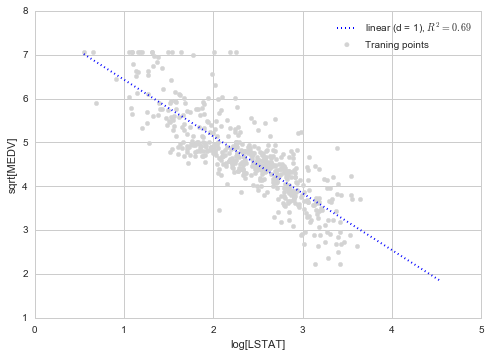
となっており、今回考慮したモデルの中では最も高い数値になっています。
まとめ
非線形効果を入れると、一般には当てはまりがよくなるが、過学習しやすくなる傾向があります。
過学習が強いのは、予測を目的とすることが多い実社会の分析では、大きなデメリットです。早い段階で線形回帰モデル程度の精度で費用対効果的に十分である、といった見立てができているのならば、無理に非線形効果を入れずに線形モデルで施策を進めるというのも手だと思います。
*1:例えば、ビジネス要件を鑑みて、プロトタイプモデルでどれくらいの精度ならモデルの磨き込みはこれくらいの期間で、最終的にはこれくらいの精度を目指す、運用に載せてどうだったらどのようにモデルを改善する、とかを議論しておくなどです。ざっくりいうと、「正解」を探すのではなく、「納得解」を見つけるためにどうするかを決めておく感じだと思います。
*2:ここはあくまで私個人の意見です。
*3:サンプリングの影響は、外れ値があることが影響しているかもしれません。外れ値の除去や、外れ値の影響を抑えるモデル構築といった方向もモデルの性能向上方針の一つです。というより、実際に自分だったらまず回帰分析前の基礎集計の時点で外れ値の対応を検討するだろうなと思います。