久々にC++を触ってみたら自明な入力しかできないのはくやしい

自明な振り返り

自明な出力しかできませんでした。
tekenuko.hatenablog.com

動機

くやしいので非自明なことを言いたい。

自明（?）なコード

自明なことを入力すると自明だと言われます。

// trivial.cpp

# include <iostream>
# include <string>
using namespace std;

int main(){
  string str;
  cout << "自明な言葉はなーんだ?" << endl;

  // 空白があっても一つのカタマリと認識させるのに使用
  getline(cin, str);

  if(str == "Hello world!"){
    cout << "自明ですね" << endl;
  } else{
    cout << "自明じゃないですね" << endl;
  }

  return 0;
}

自明な実行

trivialという実行ファイルを作って実行します。自明なクイズが始まるので、自明な入力をすると...

$ g++ -o trivial trivial.cpp 
$ ./trivial

# 出力
自明な言葉はなーんだ?  //自明なクイズが始まる
Hello world! // コマンドラインで自明に入力する
自明ですね //自明だったらしいです

非自明なことをいう

とりあえず非自明なことを言ってみます。

$ g++ -o trivial trivial.cpp 
$ ./trivial

# 出力
自明な言葉はなーんだ?  //自明なクイズが始まる
ほとんどいたるところ連続 // コマンドラインで入力する
自明じゃないですね //自明じゃなかったらしいです

非自明だったようです。よかったです。

久々にC++を触ってみたら自明なことしかできない

自明な背景

3年ぶりくらいにC++触ってみたら自明なことしかできなかったので、自明なことをしたメモをします。

自明なコード

実行すると自明な言葉を発します。

// helloworld.cpp

#include <iostream>
using namespace std;

int main(){
  cout << "Hello world!" << endl;
  return 0;
}

自明な実行

自分はコマンドライン上でコンパイルして実行するという自明なことしかできない。helloworidという実行ファイルを使って実行するという自明な営みをすると自明なことをします。

$ g++ -o helloworld helloworld.cpp 
$ ./helloworld 

# 出力
Hello world!

自明なNext Step

今の自分のC++力は自明なコードを書けるレベルとホモトピー同値です。
修行します。

Pythonでデータ分析：機械学習の自動化

導入

何か問題を解決するにあたって機械学習を活用する場合、膨大なアルゴリズム、そのアルゴリズムに付随する多くのハイパーパラメータが存在します。分析の要件が「とにかく精度、中身は問わない」だった場合、何とかして効率的にモデルとパラメータを知りたい、という状況が起こりえます*1。

そのような要件をサポートしてくれるPythonのライブラリに、auto-sklearnというものがあります。
github.com

これは、大雑把にいうと、与えられたデータを見て、scikit-learnの中から

• 良さそうな前処理の選定
• 良さそうなアルゴリズムの選定
• 良さそうなハイパーパラメータの選定

を行い、これらのアンサンブルを取る、といったことをします。

まず、Meta Learningという、データの数、種類などから、どの手法がどのデータに向いているかをモデル化し、ベイズ的最適化により最適な組み合わせを探る、そしてアンサンブルをとる、という流れです。より詳しくは、以下の論文をご参照ください。
What is auto-sklearn? — AutoSklearn 0.0.2 documentation

インストール

pip経由でインストールします。まずは、auto-sklearnを使うために必要なライブラリをインストール後、auto-sklearnをインストールします。

pip install -r https://raw.githubusercontent.com/automl/auto-sklearn/master/requirements.txt
pip install auto-sklearn

注意

auto-sklearnはUbuntuで開発されたらしく、Linuxでは動作するがMacやWindowでは動かないかもしれない、とのこと。実際、自分の環境(MacOS)で最初はうまくいきませんでした。自分の場合は、gccのバージョンが古い(4.8以前)ことが原因だったようで、バージョンを4.8以降にしたら導入できました。

コードを試したいときは

例えば、auto-sklearnのページにコード例があります。これをJupyter notebookか何かにコピーして動かしてみると良いかと思います*2。
What is auto-sklearn? — AutoSklearn 0.0.2 documentation

注意

やんちゃに動かすと大量のログを吐きながら膨大な計算をします*3。少ないデータ量でも2〜3時間はかかります。オプションでモデル探索の時間などをいじれるので、すぐに結果を見たいならオプションの指定を適切に行ったほうが良いでしょう。
APIs — AutoSklearn 0.0.2 documentation

所感

ローカルPCで動かすには、やっていることと処理時間の両方の観点でオーバースペック気味かなという感想です。使いどころとしては、ハイスペックな分析環境があり、かつどうしても精度がほしいといった場合かなと思います。

*1:個人としてはこういった中身の理解が介在しないことはしたくないですが、そういう要件の場合もありますので仕方ない。

*2:何かデモを載せようかと思いましたが、注意に書いた状況のためやめにしました（汗）。

*3:今もPCがものすごいうなりながら計算してます（汗）。

トポロジカルデータアナリシス：データと図形を結びつける

導入

不定期でトポロジカルデータアナリシス(TDA)に関する紹介をします。今回の内容は、データから図形を見立てる方法と、TDAにて登場する単体的複体の紹介をします。

データを図形に読み替える

以下の図の左側のような点の集まりを、データの集まりだとします。次に、点の周りにある半径の球を描きます*1。すると、球どうしで重なるものがでます。重なったものは、おおざっぱに「つながっている」ち見なします。すると、データは右側のような図に見立てられます。

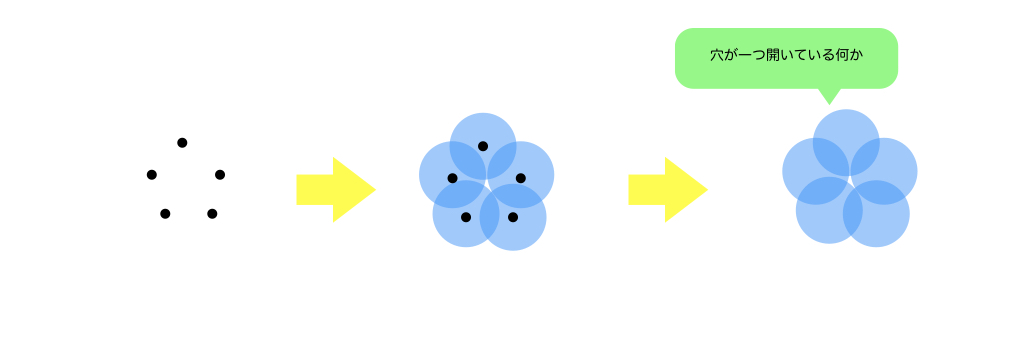
この見立てた図から何か情報が引き出せれば、それはデータの持つ大事な性質と関係しているかもしれません。

問題点

情報の引き出し方はいずれ紹介するとして、実際に引き出すにあたって以下の問題があります。

1. 見立てた図形をコンピュータで解析することは難しい

見立てた図は人間が「何となくこんな感じ」と考えたもので、細かくみると変てこりんな形をしています。そのため、こういった複雑な形のうまく計算するように実装するのは大変です。そのため、実際の計算では工夫が必要になります。

実際に解析するのは抽象単体複体

実際に計算するために有効なのが抽象単体複体です。大雑把な流れとしては、点の周りにある領域を考え、つながり方から抽象単体複体、およびその幾何学的実現（図形）*2を構成します。これは、点と線や三角形といった図形の組み合わせとなっており、コンピュータで計算することが比較的容易です*3。つまり、見立てた図形を何らかのルールによって三角形的な図形で分割して近似する、ということを（大雑把には）やっています。何らかのルールの部分は幾つか種類がありえますが、以下で代表的な3つの方法を紹介します。

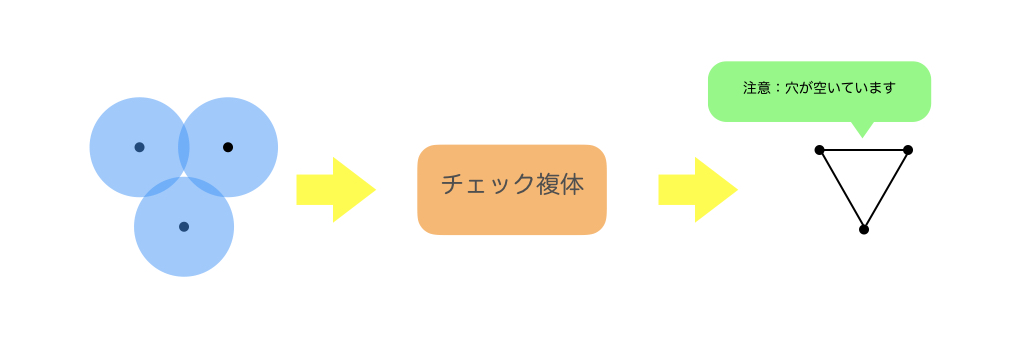
チェック複体

最も素直な構成の仕方です。

チェック複体を作る流れ

1. 点の周りにある半径の球を描く
2. 球が接していたら「つながっている」とみなし、抽象単体複体（チェック複体）を構成する
   • 抽象単体複体を構成するルール例（ざっくり）
     • 2つの球が重なる：2つの点でラベルされる1単体が抽象単体複体の要素
     • 3つの球が重なる：3つの点でラベルされる2単体が抽象単体複体の要素

ヴィートリス・リップス複体

チェック複体は、最も素直な構成の仕方ですが、計算量が多いという欠点があります。それは、何個の球が重なっているかをすべて洗い出す必要があるからです。考える点の数が増えると、考慮する場合の数も爆発的に増えてしまいます。そこで、チェック複体の簡易版として、以下のヴィートリス・リップス複体というものも考えられています。

ヴィートリス・リップス複体を作る流れ

1. 点の周りにある半径の球を描く
2. 球が接していたら「つながっている」とみなし、抽象単体複体（ヴィートリス・リップス複体）を構成する
   • チェック複体との違い
     • 個の球の「任意の」2点が重なっていれば、単体が抽象単体複体の要素
     • チェック複体は、個の球すべてが重なっている領域がないとダメ

注意点

あくまでチェック複体の簡易版であり、もとの調べたい図形と性質が変わる場合があります。以下に、その具体例を載せます。左側は穴が一つ空いている図と見なせそうですが、そこからチェック複体の幾何学的実現を構成したもの（右側）は、穴の空いていない図になります。TDAでは穴の数が本質的な量であると見なしており、両者の性質は異なることになります。

アルファ複体

ちょっと構成法が複雑ですが、計算量がチェック複体ほど多くならなそうな単体的複体です*4。

アルファ複体を作る流れ

1. 点と点の間を垂直2等分線で分割する。ただし線を引くのは他の垂直2等分線とぶつからない部分だけ
2. 各点がボロノイ領域というもので分割される*5
3. さらに点の周りにある半径の球を描き、ボロノイ領域と球の共通部分を考える
4. 上で考えた共通部分どうしが接していたら「つながっている」とみなし、抽象単体複体（アルファ複体）を構成する
   • ルールはチェック複体と同じ

なぜ抽象単体複体を調べればよいのか

これまで、TDAで登場する単体的複体についてざっと紹介しました。しかし、なぜこれらの単体的複体で近似すればよいかについては何も言っていませんでした。実は、点の周りに描く領域を凸集合に（球は凸集合）し、個の球が重なっているときに単体が要素になる（チェック複体とアルファ複体）ような抽象単体複体は、もとの見立てた図と定性的な性質が同じである*6ことが保証されています。保証する定理は、脈体定理といいます。この脈体定理があるので、TDAで知りたいような「定性的な量」は

1. いったん抽象単体複体の幾何学的実現の世界にいき、そこで必要な量を求める
2. 脈対定理より、抽象単体複体で求めた量が見立てた図で必要だった量と等しい

という手順で求めればよいということになります。ただし、ヴィートリス・リップス複体に関しては、脈対定理の前提を満たしていません。なので必ずしももとの見立てた図とヴィートリス・リップス複体の幾何学的実現の性質は一致しないことに注意です。

脈体定理に関しては、例えば
www.kyoritsu-pub.co.jp
に概要が載っています。証明までは載っていないので、気になる方は位相幾何学の本を読むとよいと思います*7。

残された疑問点

今回、データから図形を見立てる方法と、トポロジカルデータアナリシス（TDA）にて登場する単体的複体の紹介をしました。しかしながら、以下のような疑問点がまだ残っています。

• 見立てた図形から、何がわかるのか
• 点の周りに描く円の半径を変えたら、見立てられる図形も変わるけど、それは何を意味しているのか

一つ目を知るには、ホモロジー群、二つ目を知るにはパーシステントホモロジー群という数学的な対象を知る必要があります。これらをつぶさに紹介するのは非常に大変なため、詳しい説明は省略します*8。一つ目は、大雑把には図形の穴の数を抽出するイメージです*9。
tekenuko.hatenablog.com

二つ目は、TDAにてノイズ込みのデータからどうやって情報を抽出するかの部分と関係するものです。次回は、その工夫の仕方をざっくり紹介しようと考えています。

*1:必ずしも球である必要はないです。

*2:幾何学的実現は、抽象単体複体の要素の和集合（つまり、くっつけれる単体を全部くっつけた図形)です。

*3:ここの言い回しは、実際のアルゴリズムやその他の手法などを自分が理解していないため、不正確かもしれません。

*4:これは、要素として現れうる単体の次元が、アルファ複体の方が小さいことが理由の一つだと自分は思っています。実際の計算量も含めて細かいところは理解していないものがあるので、理解が深まったら都度紹介していってもアリかなと思っています。

*5:ボロノイ領域が接していた場合に「つながっている」とみなし、抽象単体複体を構成することもできます。この抽象単体複体をドロネー複体といいます。

*6:ホモトピー同値という性質です。

*7:自分は証明したことありません。。

*8:自分もきちんと理解しているかは疑問です（汗）。

*9:穴の数がわかったから何なんだ、という疑問は大いにあると思います。このあたりもそのうちうまく紹介したいものです。。

トポロジカルデータアナリシス : 単体的複体

導入

不定期でトポロジカルデータアナリシス(TDA)に関する紹介をします。今回は、私たちが普段から何気なく慣れ親しんできた図形に関する話題です。ここでは、単体的複体をいう対象を考えます。

参考

このブログでは、数式を交えた説明は基本的にしません。きちんと理解したい方は、例えば
www.kyoritsu-pub.co.jp
があります。ただし、数学科の2〜3年生くらいの知識がある程度無いと読み進めるのは難しいです。

もう少し数学科以外に向けた本としては
www.seshop.com
があります。素粒子論をやりたい学生が、何故か（ほぼ）皆が申し合わせたように学部生あたりのときに読んでいる本です。微分積分学や線形代数を理解していれば読むことは可能です。

単体

ざっくり定義

単体的複体を考えるために、その構成要素である単体から考えています。
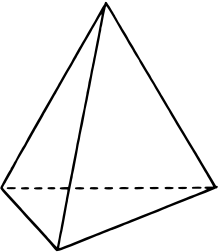
単体とは、点（0次元）や辺（1次元）、三角形（2次元）、四面体（3次元）といった図形を一般化したものです。これらをそれぞれ0次元三角形、1次元三角形、...と呼ぶことにします。これは、次元空間内の次元三角形という拡張ができます。この次元三角形を単体といいます。もう少し正確には、次元空間内に個の点を配置し、線形独立なベクトルを与え、その凸包を考える、という定式化をしますが、詳しくは参考書を参考にしていただけばと思います。

単体はより次元の低い単体を一部に含みます。それを「面」といいます。例えば、四面体（3単体）は三角形（2単体）*1や辺（1単体）、点（0単体）を一部に含んでいます。

単体的複体(複体)

ゆるゆる定義

単体的複体は、単体をあるルールによって集めた集合です。あるルールというのは、大雑把には以下の2つです。

• ある単体的複体に含まれる単体の面（部分集合的なもの）も単体的複体のメンバー
• ２つの単体が共通部分をもつときは、それぞれから見てきちんと面になっている部分で共有している

以下に、単体的複体を構成できる図形とそうでない例をあげます*2。

参考（http://infoshako.sk.tsukuba.ac.jp/~hachi/math/csc2/complex.html）

左側は三角形同士が点や辺の部分で貼り合わされていますが、右側ではそうではないものがあります。例えば、辺と点がくっついているもの（右側の図形のうち、左側）に着目します。その共通部分は点*3になっていますが、片方の三角形はそれが「面」（つまり部分集合）になっていません。つまり、2つ目の条件で、右側のようなはり合わせ方を禁止するようなルールを考えているわけです。

（注意）単体的複体は図形ではない

単体的複体は、単体をある「組み合わせ的な性質」で集めた集合であって、図形そのものではありません。そのため、ある特定の次元にある図形という具体的な対象を忘れ、集合の要素と「組み合わせ的性質」の2つだけで抽象化することが可能です。この組み合わせ的性質のみに着目したものを抽象単体複体をいいます。なんてまどろっこしいことを…と感じる方もいると思いますが、このような抽象化がデータをうまく図形に近似して特徴を取り出す際に役に立ちます。詳しい定義などは、参考書を見てください。

図形は単体的複体の幾何学的実現

では、我々が想像する図形はどう定義されているのでしょうか。これは、単体的複体に含まれるすべての要素（つまり、単体）の和集合を取ったものと定義されます。単体的複体を、その要素をとすると

が図形を表します。各単体が我々が住んでいるような空間（ユークリッド空間）にあるときは、をが定める多面体、先程簡単に紹介した抽象単体複体の世界ではをの幾何学的実現といいます。つまり、何かパーツ（単体）を組み合わせた図形を表現する際は、単体的複体を定義するだけでは不十分で、そこから幾何学的実現をとってやる必要がある、ということです。ややこしいですね。

Next Step

この単体的複体は、データという点の集まりからどうやって情報を引き出すか、を考える際に使います。次回はどのような単体的複体がトポロジカルデータアナリシスで使われるかを簡単に紹介していきます。本当は、同値とかホモトピー同値とかいう「同じ」って何ですか、ってところを考えておいたほうがよいのですが、まずは解析するのに必要なキーワード的知識を紹介していくことにフォーカスしていこうと思っています。

*1:おそらくこれが最も素朴な面のイメージだと思います。

*2:回りくどい言い方ですが、単体的複体と図形は異なるものなので、言い分けています。

*3:この言い方は実は正確ではないです。片方の三角形については面の定義を満たしていないからです。一点で交わっているという言い方のほうが良いかもしれません。