トポロジカルデータアナリシス：データと図形を結びつける

導入

不定期でトポロジカルデータアナリシス(TDA)に関する紹介をします。今回の内容は、データから図形を見立てる方法と、TDAにて登場する単体的複体の紹介をします。

データを図形に読み替える

以下の図の左側のような点の集まりを、データの集まりだとします。次に、点の周りにある半径の球を描きます*1。すると、球どうしで重なるものがでます。重なったものは、おおざっぱに「つながっている」ち見なします。すると、データは右側のような図に見立てられます。
f:id:tekenuko:20160928234459j:plain

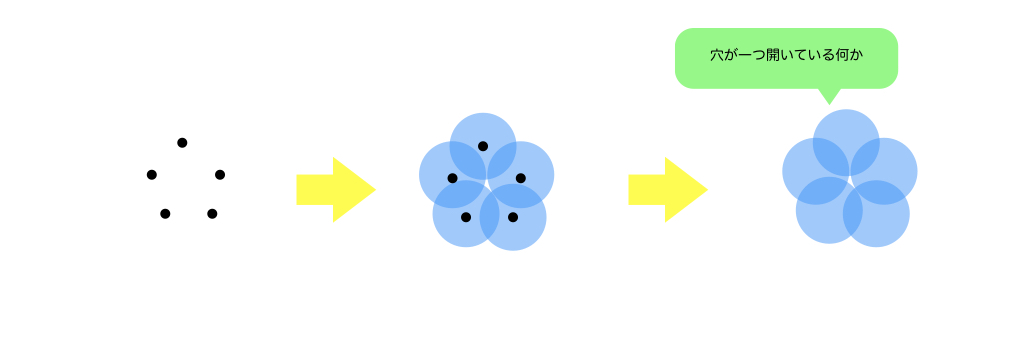
この見立てた図から何か情報が引き出せれば、それはデータの持つ大事な性質と関係しているかもしれません。

問題点

情報の引き出し方はいずれ紹介するとして、実際に引き出すにあたって以下の問題があります。

見立てた図形をコンピュータで解析することは難しい

見立てた図は人間が「何となくこんな感じ」と考えたもので、細かくみると変てこりんな形をしています。そのため、こういった複雑な形のうまく計算するように実装するのは大変です。そのため、実際の計算では工夫が必要になります。

実際に解析するのは抽象単体複体

実際に計算するために有効なのが抽象単体複体です。大雑把な流れとしては、点の周りにある領域を考え、つながり方から抽象単体複体、およびその幾何学的実現（図形）*2を構成します。これは、点と線や三角形といった図形の組み合わせとなっており、コンピュータで計算することが比較的容易です*3。つまり、見立てた図形を何らかのルールによって三角形的な図形で分割して近似する、ということを（大雑把には）やっています。何らかのルールの部分は幾つか種類がありえますが、以下で代表的な3つの方法を紹介します。

チェック複体

最も素直な構成の仕方です。

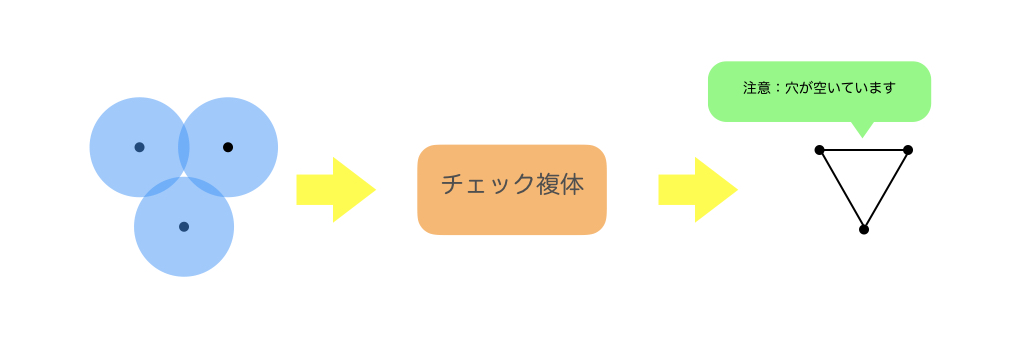
チェック複体を作る流れ

点の周りにある半径の球を描く
球が接していたら「つながっている」とみなし、抽象単体複体（チェック複体）を構成する
- 抽象単体複体を構成するルール例（ざっくり）
  - 2つの球が重なる：2つの点でラベルされる1単体が抽象単体複体の要素
  - 3つの球が重なる：3つの点でラベルされる2単体が抽象単体複体の要素

f:id:tekenuko:20160928223420j:plain

ヴィートリス・リップス複体

チェック複体は、最も素直な構成の仕方ですが、計算量が多いという欠点があります。それは、何個の球が重なっているかをすべて洗い出す必要があるからです。考える点の数が増えると、考慮する場合の数も爆発的に増えてしまいます。そこで、チェック複体の簡易版として、以下のヴィートリス・リップス複体というものも考えられています。

ヴィートリス・リップス複体を作る流れ

点の周りにある半径の球を描く
球が接していたら「つながっている」とみなし、抽象単体複体（ヴィートリス・リップス複体）を構成する
- チェック複体との違い
  - $k + 1$ 個の球の「任意の」2点が重なっていれば、 $k$ 単体が抽象単体複体の要素
  - チェック複体は、 $k + 1$ 個の球すべてが重なっている領域がないとダメ

注意点

あくまでチェック複体の簡易版であり、もとの調べたい図形と性質が変わる場合があります。以下に、その具体例を載せます。左側は穴が一つ空いている図と見なせそうですが、そこからチェック複体の幾何学的実現を構成したもの（右側）は、穴の空いていない図になります。TDAでは穴の数が本質的な量であると見なしており、両者の性質は異なることになります。
f:id:tekenuko:20160928223433j:plain

アルファ複体

ちょっと構成法が複雑ですが、計算量がチェック複体ほど多くならなそうな単体的複体です*4。

アルファ複体を作る流れ

点と点の間を垂直2等分線で分割する。ただし線を引くのは他の垂直2等分線とぶつからない部分だけ
各点がボロノイ領域というもので分割される*5
さらに点の周りにある半径の球を描き、ボロノイ領域と球の共通部分を考える
上で考えた共通部分どうしが接していたら「つながっている」とみなし、抽象単体複体（アルファ複体）を構成する
- ルールはチェック複体と同じ

f:id:tekenuko:20160928225105j:plain

なぜ抽象単体複体を調べればよいのか

これまで、TDAで登場する単体的複体についてざっと紹介しました。しかし、なぜこれらの単体的複体で近似すればよいかについては何も言っていませんでした。実は、点の周りに描く領域を凸集合に（球は凸集合）し、 $k+1$ 個の球が重なっているときに $k$ 単体が要素になる（チェック複体とアルファ複体）ような抽象単体複体は、もとの見立てた図と定性的な性質が同じである*6ことが保証されています。保証する定理は、脈体定理といいます。この脈体定理があるので、TDAで知りたいような「定性的な量」は

いったん抽象単体複体の幾何学的実現の世界にいき、そこで必要な量を求める
脈対定理より、抽象単体複体で求めた量が見立てた図で必要だった量と等しい

という手順で求めればよいということになります。ただし、ヴィートリス・リップス複体に関しては、脈対定理の前提を満たしていません。なので必ずしももとの見立てた図とヴィートリス・リップス複体の幾何学的実現の性質は一致しないことに注意です。

脈体定理に関しては、例えば
www.kyoritsu-pub.co.jp
に概要が載っています。証明までは載っていないので、気になる方は位相幾何学の本を読むとよいと思います*7。

残された疑問点

今回、データから図形を見立てる方法と、トポロジカルデータアナリシス（TDA）にて登場する単体的複体の紹介をしました。しかしながら、以下のような疑問点がまだ残っています。

見立てた図形から、何がわかるのか
点の周りに描く円の半径を変えたら、見立てられる図形も変わるけど、それは何を意味しているのか

一つ目を知るには、ホモロジー群、二つ目を知るにはパーシステントホモロジー群という数学的な対象を知る必要があります。これらをつぶさに紹介するのは非常に大変なため、詳しい説明は省略します*8。一つ目は、大雑把には図形の穴の数を抽出するイメージです*9。
tekenuko.hatenablog.com

二つ目は、TDAにてノイズ込みのデータからどうやって情報を抽出するかの部分と関係するものです。次回は、その工夫の仕方をざっくり紹介しようと考えています。

*1:必ずしも球である必要はないです。

*2:幾何学的実現は、抽象単体複体の要素の和集合（つまり、くっつけれる単体を全部くっつけた図形)です。

*3:ここの言い回しは、実際のアルゴリズムやその他の手法などを自分が理解していないため、不正確かもしれません。

*4:これは、要素として現れうる単体の次元が、アルファ複体の方が小さいことが理由の一つだと自分は思っています。実際の計算量も含めて細かいところは理解していないものがあるので、理解が深まったら都度紹介していってもアリかなと思っています。

*5:ボロノイ領域が接していた場合に「つながっている」とみなし、抽象単体複体を構成することもできます。この抽象単体複体をドロネー複体といいます。

*6:ホモトピー同値という性質です。

*7:自分は証明したことありません。。

*8:自分もきちんと理解しているかは疑問です（汗）。

*9:穴の数がわかったから何なんだ、という疑問は大いにあると思います。このあたりもそのうちうまく紹介したいものです。。

データサイエンティスト(仮)

元素粒子論博士。今はデータサイエンティスト（仮）。