Pythonでデータ分析:PyStanで線形回帰モデル
導入
ベイズ推定を行うための道具として、マルコフ連鎖モンテカルロ(MCMC)があります。その派生系であるハミルトニアンモンテカルロ(HMC)をベースにしたソフトウェアとして、Stanというものがよく知られています。
StanはC++ベースのソフトウェアですが、RやPythonを介しても使用することができます。今回は、PythonのインターフェースであるPyStanを使ってベイズ推定を行ってみます。
動機
Stan(特にRStan)は新人時代(2年半くらい前)に触っていたのですが、PJで機械学習の手法を使うことが多くなりあまり使わなくなり…といった感じでしばらく触れていませんでした。最近は、Pythonをベースに手を動かして幅を広げてみようと思っており、その一環としてPyStanに触れるのは良いだろうと思ったのが動機です。というわけで、基本的なことのメモ程度の紹介になると思います。
参考記事
流れを掴んだり、コードを書くに当たって、以下の記事が参考になりました。
qiita.com
使用データセット:Boston
久しぶりにボストン近郊の住宅情報のデータを使用します。
import sklearn from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split Boston = load_boston() X = Boston.data y = Boston.target # 学習用・検証用にデータを分割 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
Stan部分
Stanに渡す部分を以下のように書きます。
# データ(辞書型) dat = {'N': X_train.shape[0], 'M': X_train.shape[1], 'X': X_train, 'y': y_train} # Stanコード model = """ data { int<lower=0> N; int<lower=0>M; matrix[N, M] X; vector[N] y; } parameters { real beta_0; vector[M] beta; real<lower=0> sigma; } model { for (i in 1:N) y[i] ~ normal(beta_0 + dot_product(X[i] , beta), sigma); } """
モデルに与えるデータは辞書型に変更しておきます。
Stanのコードは大まかに以下の3つの部分に分かれています。
- data
- parameters
- 推定するパラメータを定義します。ここも説明変数が多いときは、vectorで係数を与えるとコードがすっきりします。
- model
コンパイル
モデルをコンパイルします。結果はstmというオブジェクトにもたせておきます。
%time stm = StanModel(model_code=model) # 計算時間 CPU times: user 1.11 s, sys: 64 ms, total: 1.18 s Wall time: 1min 21s
計算時間も一緒に表示させていましが、1分半くらいかかっています(意外とかかるな。。)。
MCMC
サンプリングを実行します。iterationの回数は5000, 初期のiterationは安定的でないことが多いので推定には使わないことが多いのですが、使わないstep(n_warmup)は1000、マルコフ連鎖の数は2(特に大きな理由はないが)としています。
n_itr = 5000 n_warmup = 1000 chains = 2 # サンプリングの実行 %time fit = stm.sampling(data=dat, iter=n_itr, chains=chains, n_jobs=-1, warmup=n_warmup, algorithm="NUTS", verbose=False) # 計算時間 CPU times: user 556 ms, sys: 142 ms, total: 697 ms Wall time: 18min 50s
推定に約19分。ちょっと時間かかりますが、ローカルPCだとこんな程度でしょうか。
推定結果
パラメータの推定結果は、fitを出力させると表示できます。
fit * 出力結果 nference for Stan model: anon_model_0456a22b1cde927056973d34c99a2678. 2 chains, each with iter=5000; warmup=1000; thin=1; post-warmup draws per chain=4000, total post-warmup draws=8000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta_0 36.89 0.09 5.55 26.09 33.12 36.87 40.63 48.0 4151 1.0 beta[0] -0.11 3.9e-4 0.03 -0.18 -0.14 -0.11 -0.09 -0.05 8000 1.0 beta[1] 0.05 1.8e-4 0.01 0.02 0.04 0.05 0.06 0.08 6937 1.0 beta[2] 0.07 7.4e-4 0.07 -0.06 0.02 0.07 0.11 0.19 8000 1.0 beta[3] 2.52 0.01 1.0 0.57 1.84 2.52 3.19 4.49 8000 1.0 beta[4] -17.87 0.06 4.18 -25.99 -20.75 -17.78 -15.09 -9.63 5632 1.0 beta[5] 3.82 6.6e-3 0.47 2.91 3.5 3.83 4.14 4.74 5064 1.0 beta[6] -2.4e-3 1.6e-4 0.01 -0.03 -0.01-2.4e-3 7.7e-3 0.03 8000 1.0 beta[7] -1.34 2.7e-3 0.22 -1.76 -1.49 -1.35 -1.2 -0.91 6336 1.0 beta[8] 0.32 9.6e-4 0.07 0.17 0.27 0.32 0.37 0.46 5900 1.0 beta[9] -0.01 5.4e-5 4.2e-3 -0.02 -0.02 -0.01 -0.01-5.7e-3 6138 1.0 beta[10] -0.98 2.0e-3 0.14 -1.26 -1.08 -0.98 -0.89 -0.7 5230 1.0 beta[11] 8.6e-3 3.2e-5 2.9e-3 2.9e-3 6.7e-3 8.6e-3 0.01 0.01 8000 1.0 beta[12] -0.51 7.1e-4 0.06 -0.62 -0.55 -0.51 -0.47 -0.4 6223 1.0 sigma 4.61 1.9e-3 0.17 4.3 4.49 4.61 4.72 4.95 8000 1.0 lp__ -817.4 0.05 2.77 -823.7 -819.0 -817.1 -815.4 -812.9 3431 1.0 Samples were drawn using NUTS at Sat Oct 14 13:21:41 2017. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).
各パラメーターごとに平均、標準誤差、標準偏差、各パーセンタイル等を見ることができます。尤度に関する情報(lp__)もリストの一番下にあります。サンプリング結果の収束を判定する値として、Rhatというものがあり、Rhatが1.1以下だと十分収束していると判断できるようです。今回はすべての係数がRhat1.0となっているので、収束していると判断します。
推定結果の可視化
大雑把にはPyStanのplotメソッドで可視化できます。
fit.plot()
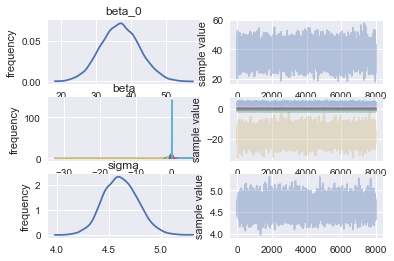
説明変数を行列で与えたのが災いして、係数の分布が見づらくなっています。そのため、もう少しわかりやすく可視化します。
# サンプル列を抽出 la = fit.extract(permuted=True) # パラメーター名 names = fit.model_pars # パラメーターの数 n_param = np.sum([1 if len(x) == 0 else x[0] for x in fit.par_dims]) # プロット f, axes = plt.subplots(n_param, 2, figsize=(15, 4*n_param)) cnt = 0 for name in names: dat = la[name] if dat.ndim == 2: for j in range(dat.shape[1]): d = dat[:,j] sns.distplot(d, hist=False, ax=axes[cnt, 0]) sns.tsplot(d, alpha=0.8, lw=.5, ax=axes[cnt, 1]) cnt += 1 else: # Intercept sns.distplot(dat, hist=False, ax=axes[cnt, 0]) sns.tsplot(dat, alpha=0.8, lw=.5, ax=axes[cnt, 1]) cnt += 1 name_list = [] for name in names: dat = la[name] if la[name].ndim == 2: for i in range(dat.shape[1]): name_list.append("{}{}".format(name,i+1)) else: name_list.append(name) for i in range(2): for j, t in enumerate(name_list): axes[j, i].set_title(t) plt.show()
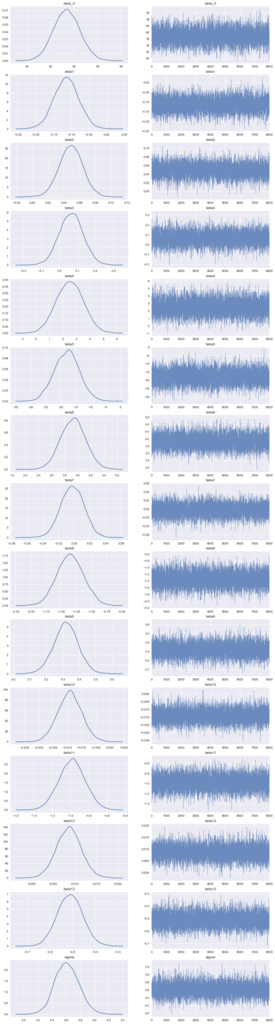
まあ概ね推定できているでしょう。分布的に幾つかは効果がほぼない変数もあるようです。精度や解釈性を向上させたい場合は、そのような変数はモデルから削除することもありますが、ここではこのまま進めます。
精度評価
得られた係数を用いて学習用・検証用データに対して予実比較を行います。今回は、簡単に係数の分布の平均値を推定された係数の値として予測値算出をします。
# 平均値算出 beta0 = la['beta_0'].mean() beta = la['beta'].mean(axis = 0) # 予測値算出 y_pred_train = (X_train * beta).sum(axis = 1) + beta0 y_pred_test = (X_test * beta).sum(axis = 1) + beta0 # 学習用、検証用データに関してMSEとR^2を出力 from sklearn.metrics import mean_squared_error, r2_score print('MSE Train: %.2f, MSE Test: %.2f' % (mean_squared_error(y_train, y_pred_train), mean_squared_error(y_test, y_pred_test))) print('R^2 Train: %.2f, R^2 Test: %.2f' % (r2_score(y_train, y_pred_train), r2_score(y_test, y_pred_test))) # 出力結果 MSE Train: 20.41, MSE Test: 28.30 R^2 Train: 0.75, R^2 Test: 0.70
以前自分が書いたsklearnを使った線形回帰モデルの記事では、R^2 Train : 0.763, Test : 0.659となっていました。データの分割の仕方に依存しそうですが、検証用に関しては若干R^2が改善しています。
tekenuko.hatenablog.com