データサイエンティスト(仮)

元素粒子論博士。今はデータサイエンティスト（仮）。

KerasでDeep Learning：とりあえずネットワークを組んでみる

Python Deep Learning Keras

導入

前回はKerasを導入しました。
tekenuko.hatenablog.com

今回は、実際にネットワークを組んで学習をさせてみようと思います。簡単すぎるような気がしますが一歩ずつ…。

データセット

人工的に乱数を振って作成したものを用います。

import numpy as np
# 784次元のベクトルを1000個生成、成分は一様乱数
data = np.random.random((1000, 784))
# 0-9の数値をランダムに1000個生成
labels = np.random.randint(10, size=(1000, 1))

Kerasでは、ラベルはone-hot encoding(一つの成分が1で、他は0の列)で表す必要があります。必要なメソッドインポートして変換します。

from keras.utils.np_utils import to_categorical
labels = to_categorical(labels, 10)

ネットワーク作成

実際にちょこざいなネットワークを構築してみます。Kerasのよいところの一つに、ネットワーク作成部分が容易かつ分かりやすいということがあります。書き方ですが、大きく2通りあるようなので、同じネットワークと2通りの方法で書いてみます。

Sequentialモデル

入力層から順繰りレイヤーを足していくような書き方をするものです。まず、今回必要なライブラリをインポートします。

from keras.models import Sequential
from keras.layers import Dense, Activation

model = Sequential()で初期化し、model.add()でネットワークを足していきます。

model = Sequential()
model.add(Dense(64, activation='relu', input_shape = (784, )))
model.add(Dense(64, activation='relu'))
model.add(Dense(10, activation='softmax'))

ネットワークの次元や活性化関数は以下です。

  • 1層目：全結合、入力784次元、出力64次元、活性化関数ReLU
  • 2層目：全結合、入力64次元、出力64次元、活性化関数ReLU
  • 2層目：全結合、入力64次元（たぶん）、 出力10次元、活性化関数SoftMax

活性化関数は以下のものを使用できます。

  • softplus
  • softsign
  • relu
  • tanh
  • sigmoid
  • hard_sigmoid
  • linear

より高度な活性化関数は、Advanced Activations Layers - Keras Documentationを参照ください。例えば、leaky_reluを使いたい場合は

from keras.layers.advanced_activations import LeakyReLU
leaky_relu = LeakyReLU()

などとしてactivation=leaky_reluとします。

モデルのコンパイルをmodel.compileで行います。

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

暗にいくつかデフォルトの引数を使っていますが、指定できるオプションは例えば以下です。

  • loss : 損失関数
    • mean_squared_error : 二乗誤差
    • mean_absolute_error : 絶対誤差
    • mean_absolute_percentage_error, make : 正解とのズレ(絶対値)の割合
    • mean_squared_logarithmic_error, msle : 正解とのズレ(二乗誤差)の割合
    • squared_hinge : マイナスのところは0, プラスは二乗誤差
    • hinge : マイナスのところは0, プラスは絶対値
    • binary_crossentropy : logloss
    • categorical_crossentropy : マルチクラスlogloss
    • sparse_categorical_crossentropy : スパースラベルを取る categorical_crossentropy
    • kullback_leibler_divergence, kld : 分布の距離（的なもの）
    • poisson : 予測-正解*log(予測)の平均
    • cosine_proximity : 予測と正解間のコサイン近似の負の平均
  • optimizer : 最適化関数
    • SGD
    • RMSprop
    • Adagrad
    • Adadelta
    • Adam
    • Adamax
    • Nadam
    • TFOptimizer
  • metrics : 評価指標
    • 一般にはmetrics=['accuracy']を使う

細かいのは他にもありますが、それはModelクラス (functional API) - Keras Documentationを参照ください。

学習はmodel.fit()で行います。

model.fit(x = data, y = labels)

オプション（一部）は以下です。より詳細はModelクラス (functional API) - Keras Documentationを参照ください。

  • x : 説明変数
  • y : 目的変数
  • batch_size : ミニバッチのサイズ
  • epochs : 同じデータで何回繰り返し学習するか、デフォルトは10
  • validation_split : 各epochで学習データの何パーセントをvalidation用データにするか

実行すると以下のものが出力されます。

Epoch 1/10
1000/1000 [==============================] - 0s - loss: 2.7473 - acc: 0.0970     
Epoch 2/10
1000/1000 [==============================] - 0s - loss: 2.3096 - acc: 0.0920     
Epoch 3/10
1000/1000 [==============================] - 0s - loss: 2.3065 - acc: 0.1100     
Epoch 4/10
1000/1000 [==============================] - 0s - loss: 2.2989 - acc: 0.1260     
Epoch 5/10
1000/1000 [==============================] - 0s - loss: 2.2863 - acc: 0.1310     
Epoch 6/10
1000/1000 [==============================] - 0s - loss: 2.2813 - acc: 0.1290     
Epoch 7/10
1000/1000 [==============================] - 0s - loss: 2.2456 - acc: 0.1590     
Epoch 8/10
1000/1000 [==============================] - 0s - loss: 2.2265 - acc: 0.1990     
Epoch 9/10
1000/1000 [==============================] - 0s - loss: 2.3623 - acc: 0.2040     
Epoch 10/10
1000/1000 [==============================] - 0s - loss: 2.2957 - acc: 0.2300

はい。。乱数を生成させて作ったデータなので、精度もへったくれもないです。

Functional API

こちらは、浅いネットワーク層の結果を次のネットワーク層の引数に渡してつないでいくイメージです。Chainerに近いかも。

# 必要なライブラリ
from keras.layers import Input, Dense
from keras.models import Model

こちらの場合は、以下のようにModelメソッドにin/outを入れるように書きます。

inputs = Input(shape=(784,))
x = Dense(64, activation='relu')(inputs)
x = Dense(64, activation='relu')(x)
predictions = Dense(10, activation='softmax')(x)
model = Model(inputs=inputs, outputs=predictions)

あとはSequentialの場合と同様、Modelのcompile、fitメソッドを使ってモデルをコンパイルして学習しますが、似たような感じなので省略します。ただし、こちらのfitメソッドのepoch数のデフォルトは1のようです。

感想

あまりコードを書かなくてもネットワークを構築して学習できるため、非常に便利だなと感じました。とりあえずざっくり分析したいときはKerasを使うと手早く分析できそうです。細かいことが気になったときはどうなのかはおいおい調べていくということで。

Next Step

今回はちょこざいなデータを使いましたが、もう少しまともなデータを使って勉強していこうと思います。

KerasでDeep Learning：導入

Python Deep Learning Keras

導入

年齢を重ねるにつれて、能力が落ちてきて危機感を感じています。こまめに努力しようと思います。

最近、Deep Learningを使うふりをしていて、申し訳程度にChainerを使っています。Chainerも書きやすいのですが、日本人ユーザがメインなので、Tensorflowなどと比較するとナレッジの蓄積具合がどうしても気になってしまいます。ただし、Tensorflowは慣れると良いらしい（同僚談）のですが、ちょっと導入ハードルが高いなあと二の足を踏んでいました。

と思っていたら、KerasというTensorflowやTheanoをバックエンドとしたフレームワークが良さそうとの噂（またまた同僚談）を耳にしました。さらに、最近はCNTKもバックエンドに指定できるようになっているらしく、将来はKerasがDeep Learningのフレームワークのハブ的な存在になるのでは、と思いました。そのため、Kerasをある程度使えることはDeep Learningで分析をやっていく上で無駄にはならないだろうという判断をしてます。

Keras

Kerasのページ（Keras Documentation）では、以下のような説明がされています。

Kerasは，Pythonで書かれた，TensorFlowまたはCNTK，Theano上で実行可能な高水準のニューラルネットワークライブラリです． Kerasは，迅速な実験を可能にすることに重点を置いて開発されました． アイデアから結果に到達するまでのリードタイムをできるだけ小さくすることが，良い研究をするための鍵になります．


次のような場合で深層学習ライブラリが必要なら，Kerasを使用してください:

  • 容易に素早くプロトタイプの作成が可能（ユーザーフレンドリー，モジュール性，および拡張性による）
  • CNNとRNNの両方，およびこれらの2つの組み合わせをサポート
  • CPUとGPU上でシームレスな動作

TensorFlow、Theano、CNTKのラッパー的な印象を受けます。裏ではこれらが動くけど、ユーザー側が書かなければならないコードは直感的でわかりやすくなっているようです。

インストール

私の環境は以下です。

  • MacOS Sierra, 10.12.2
  • Python3.6.1, anaconda4.4.0
  • pip 9.0.1

ある程度新しいVersionのpipが導入されていれば、pipで簡単にインストールできます。Kerasをpipで入れるとTheanoも同時にインストールされます。ここでは、TensorFlowをバックエンドで動かすことを見越してTensorflowも入れておきます。

$ pip install tensorflow
$ pip install keras

あとはPythonを起動してkerasのimportが成功すればOKです。とりあえず、現時点ではバックエンドで動くフレームワークのデフォルトがTensorflowのようです。

注意：pipのVersionが古いとTensorflowがインストールできない

以下のようなメッセージが出てきます。

# pip install tensorflow
Downloading/unpacking tensorflow
  Could not find any downloads that satisfy the requirement tensorflow
Cleaning up...
No distributions at all found for tensorflow

この場合は

$ pip install -U pip

をしてから再びpipでTensorflowを入れましょう。

littlebird.hatenablog.jp

それでもだめなら、、、環境構築をやり直し…ですかね。。

Next Step

実際に例を用いて実践します。まずはMNISTあたりで。

Memo：BoostのVersionを確認

C++ Boost

BoostのVersionを確認したいときに実行するコード

会社のサーバでとあるソフトウェアをPythonとbindingさせようとしたときに、BoostのVersionが知りたくなったので調べてみました。
以下のようなコードを作成して実行するとVersionがわかるようです。

#include <iostream>
#include <boost/version.hpp>

int main()
{
    int major = BOOST_VERSION / 100000;
    int minor = BOOST_VERSION / 100 % 1000;
    int patch = BOOST_VERSION % 100;
    std::cout << "boost version " << major << "." << minor << "." << patch
        << " or " << BOOST_LIB_VERSION << std::endl;
    return 0;
}


ただググっただけですが、ソース元はこちら。
boost/version.hpp - 1.64.0
e-kwsm.hatenablog.com

トポロジカルデータアナリシス：単体の境界

トポロジカルデータアナリシス 不定期

導入

不定期でトポロジカルデータアナリシス（TDA）に関する紹介をします。今回は単体の境界を数学的にどう表現するかを紹介します。

振り返り

前回、図形の穴は「境界」に着目することで特徴づけができそうだということを紹介しました。

tekenuko.hatenablog.com

今回は、境界をざっくり紹介していきます。その際に、これまで表記を曖昧にしてきたものを幾つか定義しておきます。

単体および向き

単体

単体とは、点（0次元）や辺（1次元）、三角形（2次元）、四面体（3次元）といった図形を一般化したものでした。これらは、N次元空間（以下、\mathbb{R}^Nと表記します）にあるk次元三角形と拡張されます。このようなk次元三角形をk単体といいます。今、k単体の頂点をv_0, v_1, \cdots v_kとした場合、k単体は|v_0 \cdots v_k|と表します。本当はいくつか条件がありますが、ここではざっくりした言い方にとどめておきます。

単体の向き

先程の記法は頂点の順序、つまり向きの情報がありませんでした。向きを明示的に表す記法として、ここでは\langle \rangleを採用します。例えば、2単体|v_0v_1v_2|で頂点の順序がv_0 \rightarrow v_1 \rightarrow v_2と決まっている場合、向きを加味した単体は\langle v_0 v_1 v_2 \rangleと書きます。さらに、ルールとして、ある頂点を隣の頂点と入れ替えた場合はマイナスがつく、というものを設定しておきます。例えば、向きがある1単体 \langle v_0 v_1 \rangleだと
\[ \langle v_0 v_1 \rangle = - \langle v_1 v_0 \rangle \]
といった具合です。上記の向きづけは、厳密には置換という数学を使って定式化をするのですが、ここでは立ち入らないことにします。

境界作用素

境界は、ざっくり言うと境界作用素という、k単体に対するある決まった演算として定義されます。もう少し厳密には、k単体のある集まりに対して定義されるものなのですが、ここではこれ以上立ち入らないことにします*1。今、向きづけられたk単体を\langle v_0 \cdots v_k \rangleとします。k単体に対する境界作用素を\partial _kとすると、その作用は
\[\partial _k \langle v_0 \cdots v_k \rangle = \sum _{i = 0}^k (-1)^i \langle v_0 \cdots \hat{v}_i \cdots v_k \rangle \]
というように定義されます。ここで、\langle v_0 \cdots \hat{v}_i \cdots v_k \rangle はk-1単体で、\hat{v_i}は頂点v_iが除かれていることを意味しています。つまり、境界作用素はk単体をk-1単体へ変える働きを持っています。しかも、ただ単に変えるだけではなく、「向き」も考慮しています。それが式中にある(-1)^iに対応しています。

境界作用素を作用させた例

1単体 \langle v_0 v_1 \rangle

\[ \partial _1 \langle v_0 v_1 \rangle = \langle v_1 \rangle - \langle v_0 \rangle\]

0単体でいうと向きづけは入ってくる方向がプラス、出て行く方向がマイナスとなっており、もともと、1単体としてはv_0 \rightarrow v_1という向きがあったことを鑑みると、境界作用素は向きを反映しつつ端っこ（0単体）を抽出していることがわかります。

2単体 \langle v_0 v_1 v_2 \rangle

\[ \partial _2 \langle v_0 v_1 v_2 \rangle = \langle v_1 v_2 \rangle - \langle v_0 v_2 \rangle + \langle v_0 v_1 \rangle = \langle v_0 v_1 \rangle + \langle v_1 v_2 \rangle + \langle v_2 v_0 \rangle\]

わかりやすくするために少し変形をしました。作用させるもとの2単体は、「反時計まわり」的な向きを持っていますが、境界作用素を作用させた結果は、その向きを反映したような端っこ（1単体の集まり）になっていることがわかります。以下に図的に表現したものを載せておきます。

f:id:tekenuko:20161213231451j:plain

境界の境界は無い

最後に、境界作用素の少しおもしろい性質を紹介します。それは、ある単体に境界作用素を2回作用させると必ず0になってしまう、というものです。2単体 \langle v_0 v_1 v_2 \rangleを例に見てみましょう。 \langle v_0 v_1 v_2 \rangleに\partial _2を作用させたものにさらに\partial _1を作用させると
\[ \partial _1 \partial _2 \langle v_0 v_1 v_2 \rangle = \partial _1 \left( \langle v_1 v_2 \rangle - \langle v_0 v_2 \rangle + \langle v_0 v_1 \rangle\right) \\ = \langle v_2 \rangle - \langle v_1 \rangle - \langle v_2 \rangle + \langle v_0 \rangle + \langle v_1 \rangle - \langle v_0 \rangle = 0\]
のように、うまく打ち消し合いが起きて0になります。これは一般のk単体でも成り立つ性質です。

境界から穴の議論をさらにするために

今回、ちょっとごまかしつつも境界を表現する境界作用素という道具を紹介しました。ただし、ここから「図形に穴が空いている」ことを議論するためには

  • 今考えている図形の大元に対応する単体的複体を明示的に考える
  • 単体を「基底」とみなすようなベクトル空間的なものを考え、その空間に対してきちんと境界作用素を考える

といったことを詰めていかなければなりません。ネタを小出しにしていっている感が満載ですが、次回以降はこれらに関係する話を紹介して行こうと考えています。

*1:ちゃんと単体的複体を定式化したり、群などの特定の演算が入っている数学的対象を考えなければならなくなるからです。

トポロジカルデータアナリシス：ホモロジー群の紹介のための準備

トポロジカルデータアナリシス 不定期

導入

不定期でトポロジカルデータアナリシス（TDA）に関する紹介をします。今回は、図形の「穴」を数学的に表現するための準備をします。具体的に表現していくのは次回以降になります。

振り返り

これまで、データから図形を見立てる方法を紹介してきました。

tekenuko.hatenablog.com
tekenuko.hatenablog.com

これまでの話では、見立てた図形から情報を抽出する方法を紹介していませんでした。ここでは、図形の「穴」に着目するという考えを採用します。この「穴」に着目するという考えを数学的に表現するもの（の一つ）がホモロジー群です。

図形の穴を表現する方法は他にもあり、例えば、ホモトピー群というものがあります。これも図形の形や穴の数を反映するような量になっています。理論物理学ではホモトピー群のほうがよく応用に使われ、例えば液晶や渦、宇宙ひもやドメインウォール*1の分類や、非線形微分方程式の特解（ソリトン解）の分類などの応用があります。ただし、ホモトピー群はホモロジー群に比べて具体的に計算することは非常に難しく、計算機などに載せた応用には向いていません。そのため、上記のような具体的な図形の分類の問題ではホモロジー群がよく用いられます。

以下では、「穴」を数学的に表現するための準備的な考え方を紹介していきます。

穴は「境界」で特徴づけられる

今回、1単体（= 辺）の集まりで穴を作る例と作らない例を見ることで、穴を数学的に表現する手がかりを得られないかを考えていきます。ここで、単体とは、点（0次元）や辺（1次元）、三角形（2次元）、四面体（3次元）といった図形を一般化したものです。これらをそれぞれ0次元三角形、1次元三角形、...と呼ぶことにします。これは、N次元空間内のk次元三角形という拡張ができます。このk次元三角形をk単体といいます。単体、およびそれを集めた単体的複体に関しては、ざっくり以下の記事でも紹介しています。

tekenuko.hatenablog.com

以下、1単体の集まりで穴を作る例（左）と作らない例（右）です。
f:id:tekenuko:20161212220610j:plain

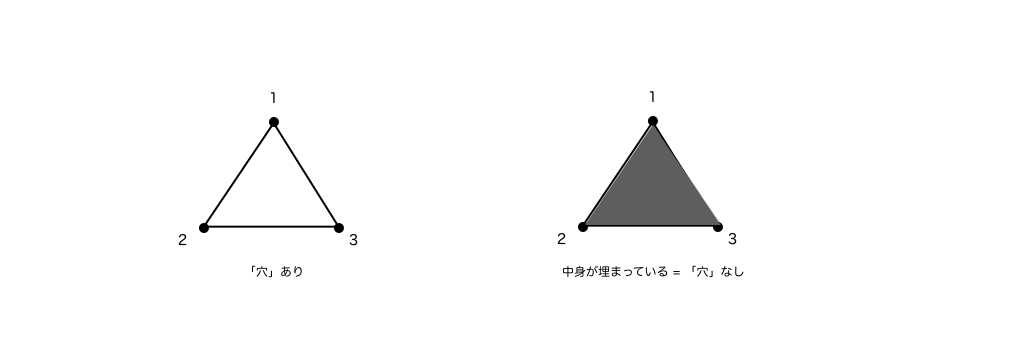
まず、左図は直感的にも穴が空いていそうですが、それはおそらく「端っこがない」ように見えるからだと思います。この「端っこ」は、数学的には「境界」と呼ばれます。例えば、頂点1と2からなる1単体の境界（端っこ）は頂点1と2です。しかしながら、頂点1と2には別の1単体（頂点1と3、および2と3からなる1単体）がくっついています。これは頂点1と3、および2と3からなる1単体に関しても同様です。つまり、これら3つの1単体の集まりには境界がありません。

一方で、右図は直感的には穴が空いていなそうです。ただし、1単体の集まりだけに着目すると、左図と構造は同じです。では、なぜ穴が空いていなそうと思うのでしょうか。

それは、1単体の中身を埋めるように2単体（三角形）が存在しているからです。これは、2単体の「端っこ」が1単体の集まりになっているとも言いかえられます。つまり、1単体の集まりに着目すると端っこを持っていませんが、この1単体の集まりは2単体の端っこになっています。

以上のことから、1単体に関しては穴を持つ条件は以下になりそうです。

「境界（端っこ）を持たない1単体の集まりで、2単体の集まりの境界になっていないもの」

つまり、ある次元の単体が与えられたとき、「境界」というものに着目すると穴による特徴づけが行なえそうです。実際、上の1単体の例を数学的に表現したものが1次ホモロジー群となっています。また、ここでの類推から、1単体をk単体、2単体をk+1単体とすればk次ホモロジー群という拡張も行えるのではないかと期待されます。

さらに数学的に定式化するために

今回は、図形の穴の分類において、「境界」というものに着目していけば良さそうであることを説明しました。次回以降、境界の数学的な表現方法を紹介していきます。ただし、そのためには単体などに関する表記や向きなどをきちんと定義した上で進める必要がある（というよりこれらを数式で表現しないと逆にわかりづらくなる）ので、以前の記事よりも若干かっちり定式化しつつ進めていきたいと思っています。

*1:これらはざっくりいうと、初期宇宙で対称性の破れによってできた一次元、二次元的な欠陥のようなものです。