データサイエンティスト(仮)

元素粒子論博士。今はデータサイエンティスト（仮）。

Pythonでデータ分析：決定木

Python scikit-learn

導入

前回、線形回帰からの拡張の一つとして、非線形項をモデルに加えることを紹介しました。
tekenuko.hatenablog.com
非線形性を表現する方法は他にも幾つかあり、その一つに、決定木という手法があります。今回は、回帰に決定木を用いた方法を紹介します。

決定木とは

まず、分類問題の文脈での決定木から定義します。決定木とは、変数に対して、分割が「お得になる」ような多数決を終了条件を満たすまで繰り返す手法です。「お得かどうか」の判断は、例えば情報の乱雑さに対応するエントロピーという量が使用されます。よりエントロピーが低い（= 分類がきれい）な条件を優先的に終了条件を満たすまで選択していきます。このように、「Xという変数がY以上」という条件でデータを分ける、といった操作が複数起こるため、その条件分岐を可視化すると、木の枝葉のような構造になります。

回帰における決定木は、上記のエントロピーの代わりに、平均二乗誤差（MSE）を指標として用います。サンプルをある条件でサブセットに分割し、それぞれのサブセットの平均値を予測値とし、MSEが減少が大きくなる分割を優先的に採用していく、といったアルゴリズムになります。そのため、予測値を可視化すると、非常に「カクカクした」（微分不可能な）振る舞いを示します。

今回は、後者の決定木回帰を議論していきます。

参考

いつものことながら、以下です。
book.impress.co.jp

データセット

今回も、前回までと同じく、ボストン近郊の住宅情報のデータを使用します。

# 必要なライブラリのインポート
import numpy as np
import pandas as pd
from pandas import DataFrame
from sklearn.datasets import load_boston
# データのロード、マージ
boston = load_boston()
df = DataFrame(boston.data, columns = boston.feature_names)
df['MEDV'] = np.array(boston.target)

モデル構築

木の分岐の深さを3に固定した場合

決定木回帰は、scikit-learnで簡単に行うことが可能です。今回は、決定木の特徴を見ることにフォーカスするために、説明変数はLSTATの一つだけに絞ります。

モデル構築は、scikit-learnのDecisionTreeRegressorクラスを用いて行うことが可能です。モデリング例は以下になります。

# 必要なライブラリのインポート
from sklearn.tree import DecisionTreeRegressor
# 説明変数と目的変数を選択
X = df.loc[:, ['LSTAT']].values
y = df.loc[:, 'MEDV'].values
# モデル構築、木の深さは3に固定
tree = DecisionTreeRegressor(max_depth = 3)
tree.fit(X, y)

散布図と回帰直線をプロットすると、以下になります。

# 回帰直線を図示するのに変数を並び替え
sort_idx = X.flatten().argsort()
# matplotlibのインポートとおまじない
import matplotlib.pyplot as plt
%matplotlib inline 

# プロット
plt.figure(figsize = (10, 7))
plt.scatter(X[sort_idx], y[sort_idx], c = 'blue', label = 'Training points')
plt.plot(X[sort_idx], tree.predict(X[sort_idx]), color = 'red', label = 'depth = 3')
plt.xlabel('LSTAT')
plt.ylabel('MEDV')
plt.legend(loc = 'upper right')
plt.show()

f:id:tekenuko:20160919205618p:plain

線形回帰や非線形回帰と比較して、カクカクした直線が引かれます。その「カクカクする」性質のため、ある程度データの傾向を補足できるのが決定木のメリットです。一方で、予測値が微分不可能になってしまう制約があるため、解析的には扱いづらい手法になっています。

木の深さと予測値の関係

先程は、木の深さを3に固定しました。木の深さを大きくすると、より複雑な条件分岐を許すことになるため、モデルの当てはまりが良くなります。しかし、それは過学習を引き起こすことにもつながるため、適切な値を選択する必要があります。

以下で、木の深さを幾つか変えた場合の予測値をプロットしています。

# あらかじめ色のリストを作成
color = ['red', 'green', 'yellow', 'magenta', 'cyan']
# for文で順繰り木の深さを変えたモデル結果をプロット
plt.figure(figsize = (10, 7))
plt.scatter(X[sort_idx], y[sort_idx], c = 'lightgray', label = 'Training points')
for t in (np.arange(5)):
        tree = DecisionTreeRegressor(max_depth = t + 1)
        tree.fit(X, y)
        sort_idx = X.flatten().argsort()
        
        plt.plot(X[sort_idx], tree.predict(X[sort_idx]), color = color[t], label = 'depth = %.1f' %(t + 1))
        plt.xlabel('LSTAT')
        plt.ylabel('MEDV')
        plt.legend(loc = 'upper right')
plt.show()

f:id:tekenuko:20160919205536p:plain

図から、木の深さが3より小さいとデータの傾向を表現しきれておらず、逆に3より大きくなると予測値が非常に複雑な振る舞いをしてしまう（過学習する）ことがわかります。今の場合は、木の深さ3がバランスがよいと判断されるでしょう。

Next Step

今回は前回までと毛色の異なった決定木の手法を紹介しました。ざっくりデータの傾向を説明できる利点がある一方、過学習の危険性を内包した手法でした。さらに、ある工夫をするより性能が高いモデルを構築できるようになるのですが、それは次回以降に紹介していこうと思います*1。

*1:というよりそれらの手法をやりたかったからあえてまず決定木を紹介したのでした。

Pythonでデータ分析：非線形効果を導入

Python scikit-learn

導入

前回、ボストン近郊の住宅情報のデータを用いて線形回帰モデルを作りました。
tekenuko.hatenablog.com

今回は、モデルの性能を上げる可能性の一つとして、多項式や指数・対数などの非線形効果をモデルに投入した場合の振る舞いを見ようと思います。

参考

前回と同様、以下の書籍を参考（写経？）にします。

book.impress.co.jp

使用するデータセット

前回と同様、ボストン近郊の住宅情報のデータを使用します。

# 必要なライブラリのインポート
import numpy as np
import pandas as pd
from pandas import DataFrame
from sklearn.datasets import load_boston
# データのロード、マージ
boston = load_boston()
df = DataFrame(boston.data, columns = boston.feature_names)
df['MEDV'] = np.array(boston.target)

非線形効果を入れる前に

非線形効果を入れる際に、（私個人の考えとして）注意する点が2つあります。

過学習に関しては、モデルの複雑さが増すことから生じます。一般に、説明変数と目的変数のデータがそれぞれn個あったとすると、n-1次の多項式を用いると残差が0で説明できてしまいます。しかしながら、このようなモデルは今のデータセットのみに強く適合するものであり、新しいデータに対する説明力が極端に低くなってしまいます。そのため、常に学習データと検証データにおける精度のバランスを見ながらモデルを評価する必要があります。

投入コストに関しては、ビジネスでのデータ分析の場面で度々考慮しなければならない問題です。実務では、納期と精度、そして費用対効果のバランスをうまくとることが求められます。非常に時間をかけて（ほんのすこし精度が向上する）非線形効果を取り入れたモデルを構築するよりも、時間をかけずに単純な（ある程度精度が担保された）モデルを作成し、早く実運用に載せて知見をためるという方が案件状況によっては良い場合があります。そのため、モデルの複雑化に関しては、要件定義や分析設計の段階でプロジェクト内での認識合わせが非常に重要になります*1。

このような注意点があるため、闇雲に変数を複雑化することはできるだけ避けたほうがよいというのが私個人の考えです。検討する場合も、事前知識を援用して判断できるもののみを考え、複雑化は最小限に留める、などします*2。

可視化

事前知識を援用する方法の一つに、データを可視化するという方法があります（あると思っています）。以下のように、変数間でどのような関係が見られるかをプロットしてみます。

# matplotlib（のなかのpyplot）をインポート
import matplotlib.pyplot as plt
# seaborn（可視化の補助を行う）のインポート
import seaborn as sns
# Jupyterを利用していたら、以下のおまじないを書くとnotebook上に図が表示
%matplotlib inline

# グラフのスタイルを指定
sns.set(style = 'whitegrid', context = 'notebook')
# 変数のペアの関係をプロット
sns.pairplot(df, size = 2.5)
plt.show()

f:id:tekenuko:20160919162755p:plain

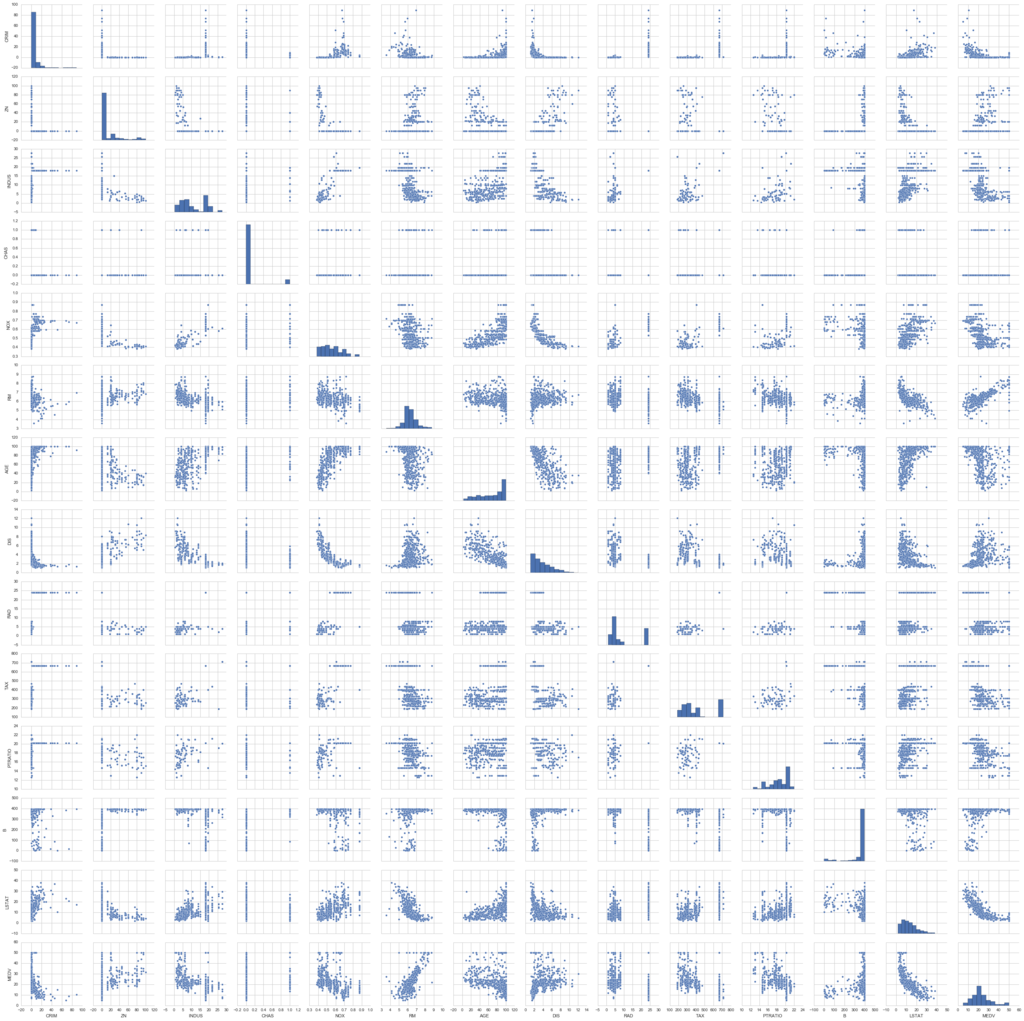
今回は、説明変数と目的変数の関係、つまり図の一番下（もしくは一番右）に着目します。
とはいえ、これでは変数が多すぎて情報過多になっています（汗）。そのため、今回フォーカスしたい部分に制限した図を以下に表示します。

# カラムを制限してプロット
sns.pairplot(df[['LSTAT', 'MEDV']], size = 2.5)
plt.show()

f:id:tekenuko:20160919163312p:plain

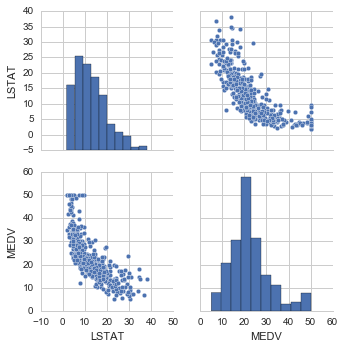
このLSTATとMEDVの散布図を見ると、直線的というよりは若干曲線的な関係性がありそうです。そのため、LSTATに関して非線形効果を導入することがモデルの性能向上に役に立つかもしれません。今回は、単純化したい理由で、説明変数はLSTATのみに絞り、モデルに投入する式を変えた場合の精度の変化を見たいと思います。

非線形効果 : 多項式

線形（1次）からの素朴な拡張として、多項式効果を入れる、という方法があります。ここでは、2次（quadratic）と3次（cubic）の項をモデルに投入した場合の精度を評価してみます。

多項式項を追加する場合、モデル構築の大枠は変更しなくても大丈夫です。

# 説明変数
X = df.loc[:, ['LSTAT']].values
# 目的変数
y = df.loc[:, 'MEDV'].values
# モデルのインスタンス生成
from sklearn.linear_model import LinearRegression
mod = LinearRegression()

変更を受けるのは、変数加工の部分です。つまり、自分で2次、3次の変数を作成し、それを代入する、ということが実際にやることです。幸い（?）、scikit-learnには非線形の変数を加工する機能がありますので、ここではそれを利用します。

多項式の変数加工は、以下のメソッドを呼び出すことで行えます。

from sklearn.preprocessing import PolynomialFeatures
# 2次（までの）変数を作成するインスタンス
quadratic = PolynomialFeatures(degree = 2)
# 3次（までの）変数を作成するインスタンス
cubic = PolynomialFeatures(degree = 3)
# 変数作成
X_quad = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)

これで多項式変数の作成ができました。

次に、線形回帰モデル、2次の項を追加、3次の項まで追加したモデルを作成します。

# モデル式用に変数を作成
X_fit = np.arange(X.min(), X.max(), 1)[:, np.newaxis]
# 線形回帰モデル、予測値、R^2を評価
mod_lin = mod.fit(X, y)
y_lin_fit = mod_lin.predict(X_fit)
r2_lin = mod.score(X, y)
# 2次の項を追加、予測値、R^2を評価
mod_quad = mod.fit(X_quad, y)
y_quad_fit = mod_quad.predict(quadratic.fit_transform(X_fit))
r2_quad = mod.score(X_quad, y)
# 3次の項を追加、予測値、R^2を評価
mod_cubic = mod.fit(X_cubic, y)
y_cubic_fit = mod_cubic.predict(cubic.fit_transform(X_fit))
r2_cubic = mod.score(X_cubic, y)

各モデルの結果をプロットします。参考のため、モデル式も重ねてプロットします。

# データ点をプロット
plt.scatter(X, y, label = 'Traning points', color = 'lightgray')
# 線形モデルのモデル式
plt.plot(X_fit, y_lin_fit, 
         label = 'linear (d = 1), $R^2=%.2f$' % r2_lin,
         color = 'blue', lw = 2, linestyle = ':')
# 2次
plt.plot(X_fit, y_quad_fit, 
         label = 'quadratic (d = 2), $R^2=%.2f$' % r2_quad, 
         color = 'red', lw = 2, linestyle = '-')
# 3次
plt.plot(X_fit, y_cubic_fit, 
         label = 'cubic (d = 3), $R^2=%.2f$' % r2_cubic,
         color = 'green', lw = 2, linestyle = '--')
plt.xlabel('LSTAT')
plt.ylabel('MEDV')
plt.legend(loc = 'upper right')
plt.show()

f:id:tekenuko:20160919181952p:plain

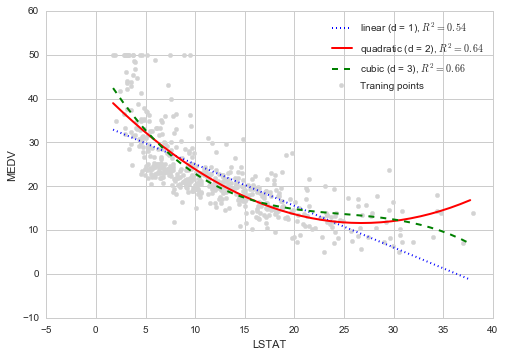
結果を見ると、3次の項まで追加した場合が最も当てはまりのよいモデルになっていることがわかります。

学習用データと検証用データで分割

前回の精度検証と同様、今回も学習用データと検証用データに分割して性能を判断してみます。

# 必要なメソッドのインポート
from sklearn.cross_validation import train_test_split
# 学習用70%、検証用30%に分割
(X_train, X_test, y_train, y_test) = 
train_test_split(X, y ,test_size = 0.3, random_state = 666)
(X_quad_train, X_quad_test, y_train, y_test) = 
train_test_split(X_quad, y , test_size = 0.3, random_state = 666)
(X_cubic_train, X_cubic_test, y_train, y_test) = 
train_test_split(X_cubic, y , test_size = 0.3, random_state = 666)

それぞれのモデルでのMSEと R^2は以下になります。

線形モデル
# モデル作成
mod.fit(X_train, y_train)
y_train_pred = mod.predict(X_train)
y_test_pred = mod.predict(X_test)
# 必要なメソッドのインポート
from sklearn.metrics import mean_squared_error
# 学習用、検証用データに関して平均二乗誤差を出力
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 学習用、検証用データに関してR^2を出力
print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_train, y_train), mod.score(X_test, y_test)))

# 出力
>>>print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
MSE Train : 42.126, Test : 30.120
>>>print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_train, y_train), mod.score(X_test, y_test)))
R^2 Train : 0.532, Test : 0.578
2次の項を追加
# モデル作成
mod.fit(X_train, y_train)
y_train_pred = mod.predict(X_quad_train)
y_test_pred = mod.predict(X_quad_test)
# 必要なメソッドのインポート
from sklearn.metrics import mean_squared_error
# 学習用、検証用データに関して平均二乗誤差を出力
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 学習用、検証用データに関してR^2を出力
print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_quad_train, y_train), mod.score(X_quad_test, y_test)))

# 出力
>>>print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
MSE Train : 32.211, Test : 26.241
>>>print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_quad_train, y_train), mod.score(X_quad_test, y_test)))
R^2 Train : 0.642, Test : 0.632
3次の項を追加
# モデル作成
mod.fit(X_train, y_train)
y_train_pred = mod.predict(X_cubic_train)
y_test_pred = mod.predict(X_cubic_test)
# 必要なメソッドのインポート
from sklearn.metrics import mean_squared_error
# 学習用、検証用データに関して平均二乗誤差を出力
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 学習用、検証用データに関してR^2を出力
print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_cubic_train, y_train), mod.score(X_cubic_test, y_test)))

# 出力
>>>print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
MSE Train : 29.914, Test : 26.968
>>>print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_cubic_train, y_train), mod.score(X_cubic_test, y_test)))
R^2 Train : 0.668, Test : 0.622

検証用データも含めて判断すると

  • 線形モデルは最も汎化性能は高い（?）が、当てはまりが悪い
  • 3次の項を追加すると過学習が高まるが、当てはまりは良い
  • 汎化性能と過学習の観点では、この中では2次のモデルが一番バランスが良い（?）

という傾向があるように見えます。

結局どうなのか

さらに調べるとわかるのですが、先程の結論（的なもの）には落とし穴があります。実は、先程の結果は、サンプリングにかなり依存しており（つまりseed値を変えたときの学習用データと検証用データのR^2の差の変化が激しい）、2次の項を加えたモデルは学習用データでのR^2のほうが検証用データでのR^2より大きいといった傾向が見えます。逆に、線形モデルはサンプリングを変えても多くの場合、過学習が弱い傾向があります。というわけで、サンプリングも含めると以下の結論になると思われます*3。

  • 線形モデルは最も汎化性能は高いが、当てはまりが悪い
  • 非線形項（2次、3次）を追加すると過学習が強くなるが、当てはまりは良くなる

他の非線形効果

多項式以外の投入方法として、指数、対数、平方根をとるといった方法があります。今回のデータだと、LSTATの対数をとり、MEDVの平方根をとる、という操作を行うとよりモデルの当てはまりがより向上します。結果をプロットすると以下のようになります。

# 非線形変換
X_log = np.log(X)
y_sqrt = np.sqrt(y)
# 線形回帰モデル作成、R^2計算
X_fit = np.arange(X_log.min(), X_log.max() + 1, 1)[:, np.newaxis]
mod_log = mod.fit(X_log, y_sqrt)
y_sqrt_fit = mod_log.predict(X_fit)
r2_sqrt = mod.score(X_log, y_sqrt)
# プロット
plt.scatter(X_log, y_sqrt, label = 'Traning points', color = 'lightgray')
plt.plot(X_fit, y_sqrt_fit, 
         label = 'linear (d = 1), $R^2=%.2f$' % r2_sqrt,
         color = 'blue', lw = 2, linestyle = ':')
plt.xlabel('log[LSTAT]')
plt.ylabel('sqrt[MEDV]')
plt.legend(loc = 'upper right')
plt.show()

f:id:tekenuko:20160919193235p:plain

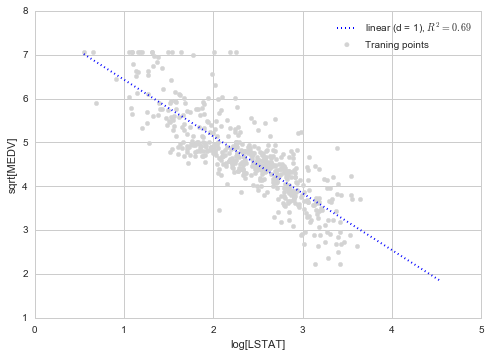
R^2 = 0.69となっており、今回考慮したモデルの中では最も高い数値になっています。

まとめ

非線形効果を入れると、一般には当てはまりがよくなるが、過学習しやすくなる傾向があります。
過学習が強いのは、予測を目的とすることが多い実社会の分析では、大きなデメリットです。早い段階で線形回帰モデル程度の精度で費用対効果的に十分である、といった見立てができているのならば、無理に非線形効果を入れずに線形モデルで施策を進めるというのも手だと思います。

*1:例えば、ビジネス要件を鑑みて、プロトタイプモデルでどれくらいの精度ならモデルの磨き込みはこれくらいの期間で、最終的にはこれくらいの精度を目指す、運用に載せてどうだったらどのようにモデルを改善する、とかを議論しておくなどです。ざっくりいうと、「正解」を探すのではなく、「納得解」を見つけるためにどうするかを決めておく感じだと思います。

*2:ここはあくまで私個人の意見です。

*3:サンプリングの影響は、外れ値があることが影響しているかもしれません。外れ値の除去や、外れ値の影響を抑えるモデル構築といった方向もモデルの性能向上方針の一つです。というより、実際に自分だったらまず回帰分析前の基礎集計の時点で外れ値の対応を検討するだろうなと思います。

Pythonでデータ分析：線形回帰モデル

Python scikit-learn

導入

データ分析にて、最も基本的な回帰分析から始めていきます*1。回帰分析とは、説明したい変数（目的変数）とそれを説明するための変数（説明変数）の間の関係を求める手法です。機械学習の手法の区分としては、教師あり学習（解答に相当する教師データを用いてモデルを構築）に属するものです。

回帰分析の目的は大きく2種類あります。

  • 理解：文字通り、変数間の構造・関係の理解
    • 例：ある病気に対して、どのような遺伝子が寄与しているかをマイクロアレイデータなどのデータを用いて明らかにする
  • 予測：変数間の関係をもとに、将来予測をする
    • 例：過去の広告の投下量と売上実績から、これらの関係を説明するモデルを構築し、それをもとに将来の広告への投資計画を立てる

ビジネスの世界では、予測を目的に使用されることがほとんどです。それは、モデル構築によって要因を明らかにするだけでなく、その後の施策でそのモデルの知見を使い、価値を生み出すことが求められるからです。逆に、アカデミックでは理解が目的の研究も一定数あります。実務でデータ分析をやっている方は、例えば、マーケティングサイエンス学会に参加するとこのあたりの思想の違いを感じ取れて面白いと思います。

使用するデータセット

ボストン近郊の住宅情報のデータを使用します。こちらは、無償で提供されており、例えばUCI Machine Learning Repository(UCI Machine Learning Repository: Housing Data Set)からダウンロードすることが可能です。ここでは、scikit-learnからロードする形で導入します。

## 必要なライブラリのインポート
from pandas import DataFrame
from sklearn.datasets import load_boston

## データの用意
# ボストンデータをインポート
boston = load_boston()
# 説明変数たちをDataFrameへ変換
df = DataFrame(boston.data, columns = boston.feature_names)
# 目的変数をDataFrameへ追加
df['MEDV'] = np.array(boston.target)

DataFrameという形式で保持するために、pandasを導入しています。最初の数行を表示してみます。

# 最初の5行を表示
df.head()

# コンソールでの表示結果
>>> df.head()
      CRIM    ZN  INDUS  CHAS    NOX     RM   AGE     DIS  RAD    TAX  
0  0.00632  18.0   2.31   0.0  0.538  6.575  65.2  4.0900  1.0  296.0   
1  0.02731   0.0   7.07   0.0  0.469  6.421  78.9  4.9671  2.0  242.0   
2  0.02729   0.0   7.07   0.0  0.469  7.185  61.1  4.9671  2.0  242.0   
3  0.03237   0.0   2.18   0.0  0.458  6.998  45.8  6.0622  3.0  222.0   
4  0.06905   0.0   2.18   0.0  0.458  7.147  54.2  6.0622  3.0  222.0   

   PTRATIO       B  LSTAT  MEDV  
0     15.3  396.90   4.98  24.0  
1     17.8  396.90   9.14  21.6  
2     17.8  392.83   4.03  34.7  
3     18.7  394.63   2.94  33.4  
4     18.7  396.90   5.33  36.2

全部で14個のカラムがありますが、今回は最初の13個を説明変数、14個目を目的変数として使用することを想定しています。それぞれのカラムにある情報は以下です。

  • CRIM : 犯罪発生率（人口単位）
  • ZN : 25000平方フィート以上の住宅区間の割合
  • INDUS : 非小売業の土地面積の割合（人口単位）
  • CHAS : チャールズ川沿いかどうかフラグ（川沿いなら1、そうでなければ0）
  • NOX : 窒素感化物の濃度（pphm単位）
  • RM : 一戸あたりの平均部屋数
  • AGE : 1940年よりも前に建てられた家屋の割合
  • DIS : ボストンの主な5つの雇用圏までの重み付き距離
  • RAD : 幹線道路へのアクセス指数
  • TAX : 10000ドルあたりの所得税率
  • PTRATIO : 教師あたりの生徒の数（人口単位）
  • B : 1000(Bk - 0.63)^2として計算される量（Bkはアフリカ系アメリカ人居住者の割合（人口単位））
  • LSTAT : 低所得者の割合
  • MEDV : 住宅価格の中央値（単位は1000ドル）

線形回帰モデルの構築

通常はモデル構築に至るまでにデータ理解や基礎集計、データ加工といった非常に重要なステップがありますが、省略します。ここでは、目的変数をMEDV、説明変数をCRIM~LSTATとした回帰モデルを構築します。今回、目的変数は連続値とみなすことができるため、回帰モデルの中でも最も単純な、目的変数と説明変数間の関係が線形である場合を仮定します。
MEDV \sim \beta _0 + \beta _1 \times ZN + \cdots + \beta _{13} \times LSTAT + \epsilon
\beta _0, \cdots ,\beta _{13}は回帰係数と呼ばれる量で、それぞれの変数がどれだけ目的変数に寄与するかを表しています。特に、\beta _0はすべての説明変数の寄与が0の場合も残る「ベース」的な量で、切片（Intercept）とも呼ばれます。 \epsilonは残差と呼ばれる量で、各データとモデル式の「ズレ」を表します。線形回帰モデルでは、各データ点の残差の二乗を足し合わせたものを最小にするという条件のもとで、係数を求めます。

scikit-learnによる係数の推定

ここでは、いったん全データを用いて線形回帰モデルを構築（=回帰係数の推定）をします。scikit-learnにあるLinearRegressionを用いると、簡単に係数の推定が行えます。

## 説明変数と目的変数
# 説明変数
X = df.loc[:, boston.feature_names].values
# 目的変数
y = df.loc[:, 'MEDV'].values
## 必要なライブラリのインポート
from sklearn.linear_model import LinearRegression
# オブジェクト生成
mod = LinearRegression(fit_intercept = True, normalize = False, copy_X = True, n_jobs = 1)
# fit関数でパラメータ推定
mod.fit(X, y)

LinearRegressionの引数を明示的に書いてありますが、それぞれは以下の意味を持っています。

  • fit_intercept : 切片項をモデル式に入れるかどうか。デフォルト値はTrue。
  • normalize : 説明変数を正規化するかどうか。デフォルト値はFalse。
  • copy_X : メモリ内でデータを複製してから実行するかどうか。 デフォルト値はTrue。
  • n_jobs : 計算に使うジョブ数。デフォルト値は1で-1にするとすべてのCPUを使って計算。

回帰係数を出力してみます。

# 回帰係数を出力
print(mod.coef_)
print(mod.intercept_)

# 出力結果
>>>print(mod.coef_)
[ -1.07170557e-01   4.63952195e-02   2.08602395e-02   2.68856140e+00
  -1.77957587e+01   3.80475246e+00   7.51061703e-04  -1.47575880e+00
   3.05655038e-01  -1.23293463e-02  -9.53463555e-01   9.39251272e-03
  -5.25466633e-01]
>>>print(mod.intercept_)
36.4911032804

学習データ、検証データに分割して性能評価

先程は、全データを用いて回帰係数の推定を行いました。しかし、それだけだと今持っているデータ「だけ」によく当てはまるモデルを作ってしまい、予測で良い性能を発揮しない場合があります。それを確認するための方法として、パラメータ推定の際に使用しなかったデータを用いて精度検証を行う、という方法があります。ここでは、持っているデータを学習用、検証用の2種類に分割して精度検証します。

上記のような精度検証は、scikit-learnを利用すると簡単に行うことができます。

# train_test_splitをインポート
from sklearn.cross_validation import train_test_split
# 70%を学習用、30%を検証用データにするよう分割
X_train, X_test, y_train, y_test = train_test_split(X, y, 
test_size = 0.3, random_state = 666)
# 学習用データでパラメータ推定
mod.fit(X_train, y_train)
# 作成したモデルから予測（学習用、検証用モデル使用）
y_train_pred = mod.predict(X_train)
y_test_pred = mod.predict(X_test)

残差プロット

モデルの性能を見る大雑把な方法として、残差プロットがあります。これは、予測値と実際の観測値の差分を可視化し、モデルで拾いきれていない非線形性や外れ値がないか、といった観点から、残差がランダムに分布しているかをチェックする方法です。数値的に性能を評価する前に、可視化して傾向を見ておくのは重要です。残差をプロットするコードは、例えば以下になります。

# matplotlibをインポート
import matplotlib.pyplot as plt
# Jupyterを利用していたら、以下のおまじないを書くとnotebook上に図が表示
%matplotlib inline
# 学習用、検証用それぞれで残差をプロット
plt.scatter(y_train_pred, y_train_pred - y_train, c = 'blue', marker = 'o', label = 'Train Data')
plt.scatter(y_test_pred, y_test_pred - y_test, c = 'lightgreen', marker = 's', label = 'Test Data')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
# 凡例を左上に表示
plt.legend(loc = 'upper left')
# y = 0に直線を引く
plt.hlines(y = 0, xmin = -10, xmax = 50, lw = 2, color = 'red')
plt.xlim([10, 50])
plt.show()

コードの実行結果は以下のようになります。
f:id:tekenuko:20160919144249p:plain

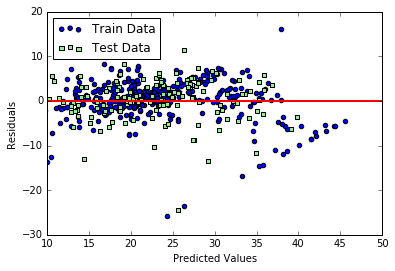
予測が完璧である場合は、残差はちょうど0になりますが、現実的にはそれはまずありません。良い回帰モデルの場合は、残差がちょうと0を中心にランダムに分布するような傾向が見えるはずです。今回のモデルに関しては、概ねランダムに分布しているようにも見えますが、学習用データを使った場合の残差に関してグラフの右下になにか直線的な傾向があり、モデルに取り切れていない情報がある可能性があります。

平均二乗誤差、決定係数

数値的にモデルの性能を評価する指標の例として、平均二乗誤差（Mean Squared Error : MSE）や決定係数（ R^2）があります。これらは、データ点を iでラベル付けしたとすると、以下のように定義されるものです。
MSE = \frac{1}{n} \sum _{i = 1}^n (y^{(i)} - y_{pred}^{(i)})^2
R^2 = 1 - \frac{MSE}{Var(y)}
MSEは、誤差の二乗和の平均値で、学習用データ、検証用データともに小さければモデルの性能が良い、と判断されます。R^2に関しては、MSEが0の場合に1をとる、つまりモデルの性能が良いほど1に近い量になります。また、R^2は学習用データに関しては0から1の値を取りますが、検証用データの場合には負の値を取ることもあります。

MSEとR^2は、scikit-learnを用いると簡単に評価できます。これらを出力するコードは、以下のようになります。

# 平均二乗誤差を評価するためのメソッドを呼び出し
from sklearn.metrics import mean_squared_error
# 学習用、検証用データに関して平均二乗誤差を出力
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 学習用、検証用データに関してR^2を出力
print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_train, y_train), mod.score(X_test, y_test)))

# 出力結果
>>>print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
MSE Train : 21.371, Test : 24.336
>>>print('R^2 Train : %.3f, Test : %.3f' % (mod.score(X_train, y_train), mod.score(X_test, y_test)))
R^2 Train : 0.763, Test : 0.659

ちなみに、R^2はsklearn.metrics.r2_scoreを呼び出して評価することも可能です。結果を見ると、学習用データのほうが検証用データよりも

  • MSEが小さい
  • R^2が大きい

という傾向があり、過学習気味のモデルであることがわかります。

モデルの磨き込み

上記の結果から、モデルの性能を上げるために、大きく２つの可能性があると考えられます。

  • モデルに非線形性を導入
  • 変数を制限する（=変数選択）

一つ目は、モデルの表現力を底上げする方向、二つ目は、過学習を緩和される方向です。次回以降は、これらの観点を取り入れて磨き込みをしていった場合にどうなるかを検討していきます。

*1:これは、分析プロジェクトでいうモデル構築のフェーズでの基本という意味です。

Pythonでデータ分析：導入

Python

背景

最近、業務でPythonを使っているのですが、不慣れな部分もありRレベルで自在に使いこなせていないと感じています*1。そのため、基本的な部分からおさらいをしていこうと考えました。

目標

試してみたいデータがあった場合に、簡単な分析に関してはとっさに手が動くレベルをまず目指します。そのために、データ加工ではnumpyとpandas（あとseries）、モデル構築ではscikit-learn、可視化ではmatplotlibとseabornを交えて紹介していくことで、この目標を実現していこうと考えています*2。

進め方

データ分析をやる上でもっとも基本的と思われる回帰分析から始めていこうと思います。基本的なことがらではありますが

  • 様々な拡張的手法のベースになっている
  • ビジネスの世界では解釈のしやすさなどの理由で回帰分析がまだまだ大事

といった理由から、このアウトプットは無駄にはならないと期待しています。

線形回帰のあとは、回帰問題だけではなく、機械学習の手法を幾つか取り上げてまとめていきます。また、単なるライブラリの使用だけでなく、可能な範囲で実装もできたらよいなと考えています。

参考文献

以下の本では、ライブラリの使い方だけでなく、実装も交えて機械学習の手法が紹介されているので、こちらを参考にしていこうと考えています*3。
book.impress.co.jp

*1:定期的にPythonは勉強しているのですが、業務ではRを使用する率が圧倒的に高かったり、携わるのが上流工程で、実分析は別担当者が…（涙）といった案件もたびたびあり、いざPythonを使おうとなったときに結構忘れてたりします。

*2:あえてブログでアウトプットすることで、記憶の定着度の向上も狙いです

*3:あくまでトレーニングが目的なので、単なる写経になってしまう可能性もありますが、ご了承ください。

Rで粒子フィルタ：RcppSMCのテスト

R 状態空間モデル

経緯

Rで粒子フィルタ（逐次モンテカルロ）ってできるんだっけ、とふと思ったので少し調べてみました。すると、Rのパッケージでは、例えば

というパッケージがあるようです。{RcppSMC}の方は、Rcppで開発されているパッケージです。まずは、簡単にテストできそうな{RcppSMC}を使ってみることにしました。

参考記事

ネットで探しているときに目についた方のブログを参考にしました。
というかほぼ丸パクリです。

d.hatena.ne.jp
ito-hi.blog.so-net.ne.jp

また、粒子フィルタに関する書籍も載せておきます。自分が読んだことあるものは、例えば以下です。ざっくり概要を知るのは樋口さんの本のほうがよさげです。
www.kspub.co.jp
時系列解析入門https://www.iwanami.co.jp/.BOOKS/00/4/0054550.htmlwww.iwanami.co.jp

テスト

パッケージのインストール

if(!require(RcppSMC)){
  install.packages("RcppSMC", dependencies = TRUE)
}
require(RcppSMC)

テストデータの生成

線形ガウス状態空間モデルのシミュレーションデータを生成します。データ点は特になんの思想もなく100点にしました。

n <- 100
sim <- simGaussian(len = n)

simはlistで、状態変数(state)と、観測データ(data)が格納されています。

プロット

無駄に{ggplot2}で描きます。

# パッケージのインストール
if(!require(ggplot2)){
  install.packages("ggplot2", dependencies = TRUE)
}
require(ggplot2)

# data.frameに変換 
df <- data.frame(iteration = 1:length(sim$state), 
                   state = sim$state, 
                   data = sim$data)

# プロット
ggplot(data = df) + 
  geom_line(mapping = aes(x = iteration, y = state), 
            colour = "magenta") + 
  geom_point(mapping = aes(x = iteration, y = data), 
             shape = 21, size = 3, colour = "blue")

f:id:tekenuko:20160903213830p:plain

観測データから状態を推定

ここでは、逆に与えられた観測データから状態変数を推定します。{RcppSMC}では、blockpfGaussianOpt関数を使用して行います。plot = TRUEとすると、自動的に図を出力してくれます。ここで、粒子数は1000としています。

blockpfGaussianOpt(sim$data, 
                   particle = 1000, 
                   lag = 5, 
                   plot = TRUE)

f:id:tekenuko:20160903214619p:plain

推定値を取り出してもとのシミュレーションデータと比較

# 推定値などを格納
res <- blockpfGaussianOpt(sim$data, 
                          particle = 1000, 
                          lag = 5, 
                          plot = FALSE)

# 推定値を取り出す
estimate <- apply(res$values, 2, mean)

# 前に作っていたdata.frameに追加
df <- cbind(df, estimate)

# プロット
ggplot(data = df) + 
  geom_line(mapping = aes(x = iteration, y = state), 
            colour = "magenta") + 
  geom_line(mapping = aes(x = iteration, y = estimate), 
            colour = "green") + 
  geom_point(mapping = aes(x = iteration, y = data), 
             shape = 21, size = 3, colour = "blue")

f:id:tekenuko:20160903215606p:plain
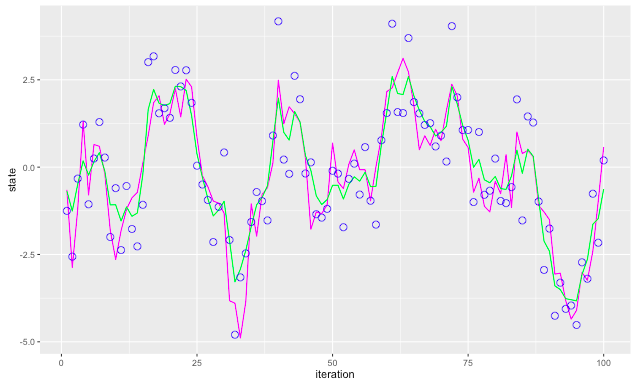
緑の線が推定値で、そこそこ推定できているとも言えなくもない結果がでてきました。

おわりに

他にもpfLineartBS、pfNonlinBSといった関数が用意されていますが、マニュアルに載っている論文の結果を再現するだけです。他のパッケージとしては、{SMC}もありますが、こちらはパッケージが2011年から更新されていないようです。こちらも後日時間があったらテストしてみたいと思っています。